a) Falso :
Seja

qualquer função contínua em
![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
( e portanto integrável sobre este intervalo) .
Suponha
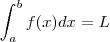
.Defina
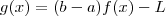
. Note que g também é continua em [a,b] e
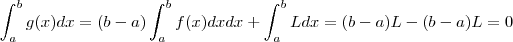
mas nem sempre

.
Exemplificando :
Dado

;
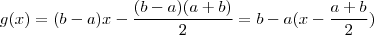
desde que o intervalo não é degenerado , g(x) = 0 sse

(b) Falso :
A função admite candidatos extremantes locais se para um subintervalo de
![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
ela
não é estritamente monótona em tal subintervalo . Por que seja fosse estritamente monótona ; das duas uma
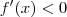
ou

levando em conta que ela é diferenciável no aberto contido em [a,b] .
Exemplo : Se
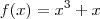
,

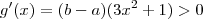
para todo x em [a,b] ; logo não admite pontos críticos .
(c) Por (b) g é crescente . ; logo afirmação falsa .
(d) Verdadeiro .
Suponha que não exista c em [a,b] tal que f(c) = 0 .Então ,
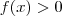
para todo x em [a,b] ou
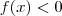
x em [a,b] . (Pois , se tivéssemos
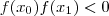
com
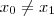
;como f é continua em pelo TVI teríamos um c entre x_1 e x_0 tq f(c) = 0 ) .
Se
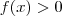
em [a,b] então
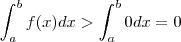
(monotonicidade da intergral )
Se
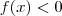
em [a,b] então
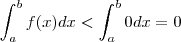
(monotonicidade da intergral )
Portanto a suposição é falsa .
É isto ; desculpe , estou com pressa e digitei na correria , bem provável alguns erros de digitação .
 [a, b] tal que, a função se anula em c;
[a, b] tal que, a função se anula em c;

 qualquer função contínua em
qualquer função contínua em ![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) ( e portanto integrável sobre este intervalo) .
( e portanto integrável sobre este intervalo) . 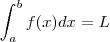 .Defina
.Defina 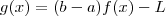 . Note que g também é continua em [a,b] e
. Note que g também é continua em [a,b] e 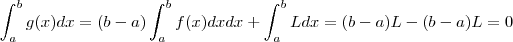 mas nem sempre
mas nem sempre  .
.  ;
; 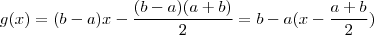 desde que o intervalo não é degenerado , g(x) = 0 sse
desde que o intervalo não é degenerado , g(x) = 0 sse 
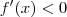 ou
ou  levando em conta que ela é diferenciável no aberto contido em [a,b] .
levando em conta que ela é diferenciável no aberto contido em [a,b] . 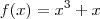 ,
, 
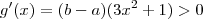 para todo x em [a,b] ; logo não admite pontos críticos .
para todo x em [a,b] ; logo não admite pontos críticos . 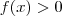 para todo x em [a,b] ou
para todo x em [a,b] ou 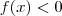 x em [a,b] . (Pois , se tivéssemos
x em [a,b] . (Pois , se tivéssemos 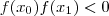 com
com 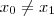 ;como f é continua em pelo TVI teríamos um c entre x_1 e x_0 tq f(c) = 0 ) .
;como f é continua em pelo TVI teríamos um c entre x_1 e x_0 tq f(c) = 0 ) . 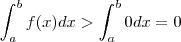 (monotonicidade da intergral )
(monotonicidade da intergral )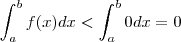 (monotonicidade da intergral )
(monotonicidade da intergral )
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.