 por Janoca » Qua Jun 18, 2014 15:27
por Janoca » Qua Jun 18, 2014 15:27
Sabe-se que a integral definida de uma função contínua, no intervalo [a, b] é nula. Pode-se concluir que:
a) A função é nula em [a, b];
b) A função tem um ponto crítico em [a, b];
c) A função não é crescente em [a, b];
d) Existe pelo menos um ponto c

[a, b] tal que, a função se anula em c;
e) Nada se pode afirmar.
Gostaria de entender o porque de cada questão falsa, como o porque da resposta correta.
Obrigada
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por e8group » Qua Jun 18, 2014 16:40
por e8group » Qua Jun 18, 2014 16:40
a) Falso :
Seja

qualquer função contínua em
![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
( e portanto integrável sobre este intervalo) .
Suponha
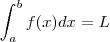
.Defina
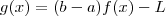
. Note que g também é continua em [a,b] e
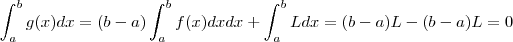
mas nem sempre

.
Exemplificando :
Dado

;
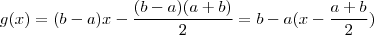
desde que o intervalo não é degenerado , g(x) = 0 sse

(b) Falso :
A função admite candidatos extremantes locais se para um subintervalo de
![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
ela
não é estritamente monótona em tal subintervalo . Por que seja fosse estritamente monótona ; das duas uma
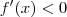
ou

levando em conta que ela é diferenciável no aberto contido em [a,b] .
Exemplo : Se
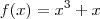
,

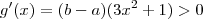
para todo x em [a,b] ; logo não admite pontos críticos .
(c) Por (b) g é crescente . ; logo afirmação falsa .
(d) Verdadeiro .
Suponha que não exista c em [a,b] tal que f(c) = 0 .Então ,
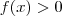
para todo x em [a,b] ou
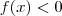
x em [a,b] . (Pois , se tivéssemos
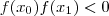
com
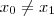
;como f é continua em pelo TVI teríamos um c entre x_1 e x_0 tq f(c) = 0 ) .
Se
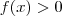
em [a,b] então
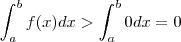
(monotonicidade da intergral )
Se
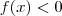
em [a,b] então
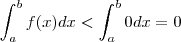
(monotonicidade da intergral )
Portanto a suposição é falsa .
É isto ; desculpe , estou com pressa e digitei na correria , bem provável alguns erros de digitação .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Jun 19, 2014 12:54
por e8group » Qui Jun 19, 2014 12:54
Só uma observação :
NO item (b) quando eu me refiro subintervalo lê-se subintervalo aberto de [a,b] .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função continua
por Amparo » Dom Mar 09, 2008 16:14
- 1 Respostas
- 3925 Exibições
- Última mensagem por admin

Qui Mar 13, 2008 12:52
Funções
-
- função continua
por alexandreredefor » Dom Jul 17, 2011 18:23
- 4 Respostas
- 3188 Exibições
- Última mensagem por Molina

Seg Jul 18, 2011 11:42
Cálculo: Limites, Derivadas e Integrais
-
- Função Contínua
por Ana Maria da Silva » Sex Mar 14, 2014 18:55
- 1 Respostas
- 1601 Exibições
- Última mensagem por Russman

Sáb Mar 15, 2014 10:45
Cálculo: Limites, Derivadas e Integrais
-
- [Função continua]
por stepg_ » Dom Set 14, 2014 13:41
- 1 Respostas
- 1669 Exibições
- Última mensagem por jcmatematica

Qui Set 25, 2014 23:27
Cálculo: Limites, Derivadas e Integrais
-
- Função contínua
por felipe_pereira96 » Qua Jan 27, 2016 12:17
- 1 Respostas
- 1798 Exibições
- Última mensagem por adauto martins

Qui Jan 28, 2016 10:00
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 [a, b] tal que, a função se anula em c;
[a, b] tal que, a função se anula em c;

 qualquer função contínua em
qualquer função contínua em ![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) ( e portanto integrável sobre este intervalo) .
( e portanto integrável sobre este intervalo) . 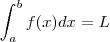 .Defina
.Defina 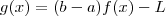 . Note que g também é continua em [a,b] e
. Note que g também é continua em [a,b] e 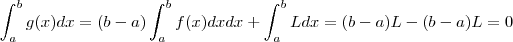 mas nem sempre
mas nem sempre  .
.  ;
; 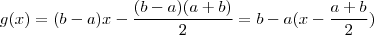 desde que o intervalo não é degenerado , g(x) = 0 sse
desde que o intervalo não é degenerado , g(x) = 0 sse 
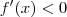 ou
ou  levando em conta que ela é diferenciável no aberto contido em [a,b] .
levando em conta que ela é diferenciável no aberto contido em [a,b] . 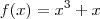 ,
, 
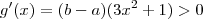 para todo x em [a,b] ; logo não admite pontos críticos .
para todo x em [a,b] ; logo não admite pontos críticos . 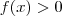 para todo x em [a,b] ou
para todo x em [a,b] ou 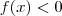 x em [a,b] . (Pois , se tivéssemos
x em [a,b] . (Pois , se tivéssemos 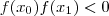 com
com 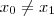 ;como f é continua em pelo TVI teríamos um c entre x_1 e x_0 tq f(c) = 0 ) .
;como f é continua em pelo TVI teríamos um c entre x_1 e x_0 tq f(c) = 0 ) . 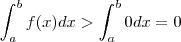 (monotonicidade da intergral )
(monotonicidade da intergral )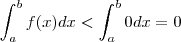 (monotonicidade da intergral )
(monotonicidade da intergral )





