 por yuricastilho » Qui Abr 10, 2014 00:15
por yuricastilho » Qui Abr 10, 2014 00:15
b) Se
![\[\lim_{x \rightarrow 0} \frac{f(x)}{x} = 0\] \[\lim_{x \rightarrow 0} \frac{f(x)}{x} = 0\]](/latexrender/pictures/75b76895235d3b073befdbf82e78b914.png)
, qual o
![\[\lim_{x \rightarrow 0} f(x)\] \[\lim_{x \rightarrow 0} f(x)\]](/latexrender/pictures/bbd640088295fcc50e04e9003084d710.png)
?
c)Se
![\[\lim_{x \rightarrow + \infty } \frac{f(x)}{x^2 + x} = +\infty\] \[\lim_{x \rightarrow + \infty } \frac{f(x)}{x^2 + x} = +\infty\]](/latexrender/pictures/147a939c177bc9c493d4b056e2c15113.png)
qual o
![\[\lim_{x \rightarrow + \infty } f(x)\] \[\lim_{x \rightarrow + \infty } f(x)\]](/latexrender/pictures/619ecc0048a89d2134f2045f2e25ce72.png)
Se alguém puder me ajudar nesses dois por favor...
-
yuricastilho
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 05, 2014 19:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por e8group » Sáb Abr 12, 2014 01:04
por e8group » Sáb Abr 12, 2014 01:04
A ideia geral é
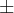
essa
Se

calcule
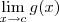
.
Um raciocínio utilizando uma das regras operatórias

. Em seguida ,calcule separadamente o limite da função h .
P.S.: c e k podem ser números bem como

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por yuricastilho » Ter Abr 15, 2014 14:31
por yuricastilho » Ter Abr 15, 2014 14:31
Obrigado Santhiago, consegui fazer agora.
-
yuricastilho
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 05, 2014 19:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Seja f(x) = (3x - 2)/(x - 2) RESOLVIDO
por yuricastilho » Sáb Abr 05, 2014 19:59
- 3 Respostas
- 1610 Exibições
- Última mensagem por yuricastilho

Dom Abr 06, 2014 22:45
Cálculo: Limites, Derivadas e Integrais
-
- [Dúvida Prática Equações] por favor alguem me responda logo.
por ArthurMoreira » Ter Fev 12, 2013 15:52
- 3 Respostas
- 1506 Exibições
- Última mensagem por DanielFerreira

Ter Fev 12, 2013 17:28
Equações
-
- (UFC) Seja f a função...
por manuoliveira » Sex Ago 27, 2010 22:20
- 2 Respostas
- 1993 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 28, 2010 17:03
Funções
-
- (ESAL) Seja AB tal que AB= a e AM/MB= 3/5.
por Gustavo R » Sex Ago 12, 2011 21:06
- 2 Respostas
- 1490 Exibições
- Última mensagem por Gustavo R

Sáb Ago 13, 2011 14:49
Geometria Plana
-
- Seja ?(x) uma função derivavel
por kak9 » Ter Out 02, 2018 15:33
- 0 Respostas
- 2975 Exibições
- Última mensagem por kak9

Ter Out 02, 2018 15:33
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\[\lim_{x \rightarrow 0} \frac{f(x)}{x} = 0\] \[\lim_{x \rightarrow 0} \frac{f(x)}{x} = 0\]](/latexrender/pictures/75b76895235d3b073befdbf82e78b914.png) , qual o
, qual o ![\[\lim_{x \rightarrow 0} f(x)\] \[\lim_{x \rightarrow 0} f(x)\]](/latexrender/pictures/bbd640088295fcc50e04e9003084d710.png) ?
?![\[\lim_{x \rightarrow + \infty } \frac{f(x)}{x^2 + x} = +\infty\] \[\lim_{x \rightarrow + \infty } \frac{f(x)}{x^2 + x} = +\infty\]](/latexrender/pictures/147a939c177bc9c493d4b056e2c15113.png) qual o
qual o ![\[\lim_{x \rightarrow + \infty } f(x)\] \[\lim_{x \rightarrow + \infty } f(x)\]](/latexrender/pictures/619ecc0048a89d2134f2045f2e25ce72.png)

![\[\lim_{x \rightarrow 0} \frac{f(x)}{x} = 0\] \[\lim_{x \rightarrow 0} \frac{f(x)}{x} = 0\]](/latexrender/pictures/75b76895235d3b073befdbf82e78b914.png) , qual o
, qual o ![\[\lim_{x \rightarrow 0} f(x)\] \[\lim_{x \rightarrow 0} f(x)\]](/latexrender/pictures/bbd640088295fcc50e04e9003084d710.png) ?
?![\[\lim_{x \rightarrow + \infty } \frac{f(x)}{x^2 + x} = +\infty\] \[\lim_{x \rightarrow + \infty } \frac{f(x)}{x^2 + x} = +\infty\]](/latexrender/pictures/147a939c177bc9c493d4b056e2c15113.png) qual o
qual o ![\[\lim_{x \rightarrow + \infty } f(x)\] \[\lim_{x \rightarrow + \infty } f(x)\]](/latexrender/pictures/619ecc0048a89d2134f2045f2e25ce72.png)

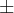 essa
essa  calcule
calcule 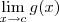 .
.  . Em seguida ,calcule separadamente o limite da função h .
. Em seguida ,calcule separadamente o limite da função h .  .
.


 .
.
 :
: