 por Riku » Ter Mar 11, 2014 01:53
por Riku » Ter Mar 11, 2014 01:53
Olá, tudo bom? Acabei de começar a faculdade e está naquele momento de relembrar, porém não consigo de jeito nenhum resolver uma questão. Uma delas eu consegui, mas vou postar apenas para vocês me ajudarem no caso de eu ter errado.
1- Determine as equações das retas suportes dos lados do triângulo cujo vértices são:
A(0,0) ; B(1,3) ; C(4,0)
Minha resposta:
AB: 3x - y = 0
AC: y = 0
BC: x + y = 4
2- Para os valores de m e k a equação mx² + y² + 4x -6y + k = 0 representa uma circunferência?
Minha resposta:
Assisti uns vídeos e cheguei nisto:
mx²+4x+y²-6y
mx²+2.2x+y²-2.3y
mx²+2.2x+2²+y²-2.3y+3²
mx²+4x+4+y²-6y+9
mx²+y²+4x-6y+13
Tem uma fórmula que anotei mas não a entendi muito bem, segue: r² = D² + E² - 4AF / 4A²
Agradeço quem puder me ajudar.
-
Riku
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mar 11, 2014 01:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciência da Computação
- Andamento: cursando
 por Russman » Ter Mar 11, 2014 23:48
por Russman » Ter Mar 11, 2014 23:48
Na 1° você obteve as equações corretas.
Na 2°, lembre-se que uma circunferência é sempre do tipo
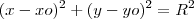
. Ou seja, expandindo
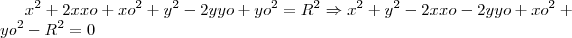
.
Agora, compare a forma expandida com a que você tem.
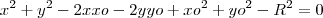

A única forma de as equações serem iguais é que
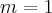

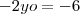

.
Solucionando, temos
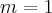
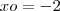


Ou seja, precisamos que
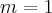
e que
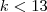
para ser possível a equação representar uma circunferência.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvidas com essas duas questões.
por Dimas » Qui Dez 09, 2010 12:42
- 0 Respostas
- 1464 Exibições
- Última mensagem por Dimas

Qui Dez 09, 2010 12:42
Binômio de Newton
-
- [Equação de reta] - duas dúvidas
por MrJuniorFerr » Sex Out 12, 2012 22:03
- 3 Respostas
- 1778 Exibições
- Última mensagem por young_jedi

Sáb Out 13, 2012 11:14
Geometria Analítica
-
- Duas cordas
por Balanar » Seg Out 18, 2010 13:05
- 2 Respostas
- 1544 Exibições
- Última mensagem por Balanar

Seg Out 18, 2010 13:35
Geometria Plana
-
- Duas questões
por caio123 » Qua Ago 24, 2011 20:22
- 0 Respostas
- 1586 Exibições
- Última mensagem por caio123

Qua Ago 24, 2011 20:22
Logaritmos
-
- Problema com duas variáveis
por helen_chaves » Qua Jun 03, 2009 12:00
- 3 Respostas
- 4123 Exibições
- Última mensagem por Cleyson007

Sex Jun 05, 2009 12:51
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


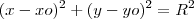 . Ou seja, expandindo
. Ou seja, expandindo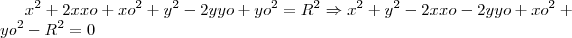 .
.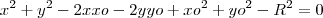

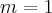

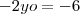
 .
.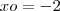


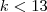 para ser possível a equação representar uma circunferência.
para ser possível a equação representar uma circunferência.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
