 por Cleyson007 » Ter Jan 28, 2014 18:42
por Cleyson007 » Ter Jan 28, 2014 18:42
Encontre os números críticos da função
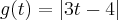
.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Man Utd » Ter Jan 28, 2014 19:44
por Man Utd » Ter Jan 28, 2014 19:44
Como sabemos da teoria que no ponto crítico a derivada é
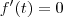
ou a derivada não existe.
Veja o gráfico da função
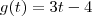
:
agora veja o gráfico da função :
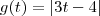
:
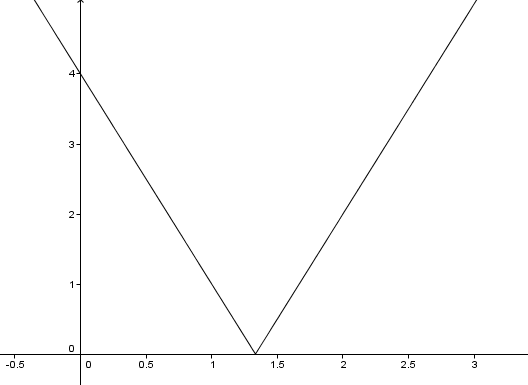
- Forum ajudmatematica 2.png (11.68 KiB) Exibido 2728 vezes
A função modular rebate a parte negativa da função, e veja que justamente depois da raiz de
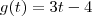
que é
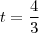
a função assume valores negativos, então a função modular rebate esta parte negativa formando uma espécie de "bico" .Nesse "bico" a função não é derivavél, se quiser confimar vc pode derivar pela definição:
Sabemos que a função módulo, é uma função definida por partes:
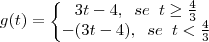
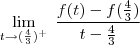
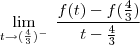
Editado pela última vez por
Man Utd em Qua Jan 29, 2014 15:45, em um total de 4 vezes.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Cleyson007 » Ter Jan 28, 2014 20:00
por Cleyson007 » Ter Jan 28, 2014 20:00
Bom, havia pensado da seguinte forma:
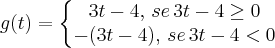
Sei também que a deriada da primeira linha dará 3 e da segunda linha dará -3, mas não conclui o raciocínio.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Russman » Ter Jan 28, 2014 23:16
por Russman » Ter Jan 28, 2014 23:16
O ponto crítico é em
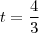
pois neste a derivada não se define e este ponto pertence ao domínio de
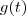
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Man Utd » Qua Jan 29, 2014 00:19
por Man Utd » Qua Jan 29, 2014 00:19
Cleyson007 escreveu:Bom, havia pensado da seguinte forma:
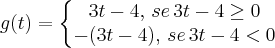
Sei também que a deriada da primeira linha dará 3 e da segunda linha dará -3, mas não conclui o raciocínio.
Vc fez a derivada em qual ponto ?
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Cleyson007 » Qua Jan 29, 2014 08:11
por Cleyson007 » Qua Jan 29, 2014 08:11
Man Utd e Russman, estou pensando da seguinte forma:
A derivada de g é representada com o intervalo aberto, logo a derivada não está definida no ponto t = 4/3 que é o ponto crítico.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Numeros criticos!!!
 por aline_n » Qua Jun 01, 2011 18:59
por aline_n » Qua Jun 01, 2011 18:59
- 1 Respostas
- 1364 Exibições
- Última mensagem por carlosalesouza

Qua Jun 01, 2011 19:19
Cálculo: Limites, Derivadas e Integrais
-
- Numeros criticos
por aline_n » Qua Jun 01, 2011 20:14
- 5 Respostas
- 4085 Exibições
- Última mensagem por carlosalesouza

Qui Jun 02, 2011 18:33
Cálculo: Limites, Derivadas e Integrais
-
- Números Críticos
por Carolwis » Sáb Nov 15, 2014 14:39
- 1 Respostas
- 1501 Exibições
- Última mensagem por adauto martins

Qua Nov 19, 2014 14:36
Cálculo: Limites, Derivadas e Integrais
-
- Números críticos da função
por Vencill » Ter Dez 02, 2014 17:38
- 1 Respostas
- 1223 Exibições
- Última mensagem por Cleyson007

Ter Dez 02, 2014 18:04
Funções
-
- Determinar os numeros criticos
por Vencill » Qua Dez 03, 2014 17:42
- 3 Respostas
- 1894 Exibições
- Última mensagem por Cleyson007

Qui Dez 04, 2014 08:21
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
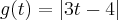 .
.

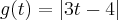 .
.
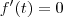 ou a derivada não existe.
ou a derivada não existe.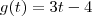 :
: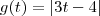 :
: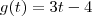 que é
que é 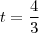 a função assume valores negativos, então a função modular rebate esta parte negativa formando uma espécie de "bico" .Nesse "bico" a função não é derivavél, se quiser confimar vc pode derivar pela definição:
a função assume valores negativos, então a função modular rebate esta parte negativa formando uma espécie de "bico" .Nesse "bico" a função não é derivavél, se quiser confimar vc pode derivar pela definição: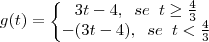
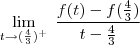
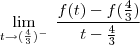

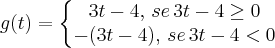

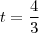 pois neste a derivada não se define e este ponto pertence ao domínio de
pois neste a derivada não se define e este ponto pertence ao domínio de 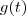 .
.

