 por Juliana Odebrech » Qua Nov 27, 2013 23:22
por Juliana Odebrech » Qua Nov 27, 2013 23:22
Como resolver esse limite através da Regra de L'Hospital:

-
Juliana Odebrech
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Nov 27, 2013 23:16
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qui Nov 28, 2013 20:36
por e8group » Qui Nov 28, 2013 20:36
Observe que a substituição
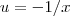
resolverá o problema (Sugestão :Veja o limite fundamental
http://en.wikipedia.org/wiki/List_of_re ... tions_of_e )
Alternativamente , definindo
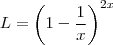
e aplicando o logaritmo natural em ambos lados ,

.Passando ao limite com
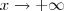
, notamos a indeterminação "0/0" ,então apliquemos regra de L'hospital e ... Tente concluir .
Tente fazer das duas formas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada regra de L'Hospital
por Wumaxeb » Sex Mai 27, 2011 22:19
- 2 Respostas
- 3115 Exibições
- Última mensagem por Molina

Sex Mai 27, 2011 23:24
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 20:26
- 2 Respostas
- 1924 Exibições
- Última mensagem por Claudin

Qui Jul 14, 2011 20:46
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 21:16
- 9 Respostas
- 3362 Exibições
- Última mensagem por MarceloFantini

Sáb Jul 16, 2011 15:20
Cálculo: Limites, Derivadas e Integrais
-
- regra de L' Hospital
por matmatco » Qua Nov 30, 2011 13:47
- 5 Respostas
- 2485 Exibições
- Última mensagem por matmatco

Sáb Dez 03, 2011 07:10
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'hospital
 por samra » Dom Ago 19, 2012 18:37
por samra » Dom Ago 19, 2012 18:37
- 1 Respostas
- 2439 Exibições
- Última mensagem por e8group

Dom Ago 19, 2012 19:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





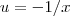 resolverá o problema (Sugestão :Veja o limite fundamental http://en.wikipedia.org/wiki/List_of_re ... tions_of_e )
resolverá o problema (Sugestão :Veja o limite fundamental http://en.wikipedia.org/wiki/List_of_re ... tions_of_e ) 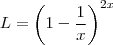 e aplicando o logaritmo natural em ambos lados ,
e aplicando o logaritmo natural em ambos lados ,  .Passando ao limite com
.Passando ao limite com 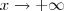 , notamos a indeterminação "0/0" ,então apliquemos regra de L'hospital e ... Tente concluir .
, notamos a indeterminação "0/0" ,então apliquemos regra de L'hospital e ... Tente concluir .