 por Danilo » Dom Nov 24, 2013 18:20
por Danilo » Dom Nov 24, 2013 18:20
Resolver
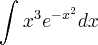
eu fiz até
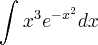

eu não sei como encontrar v. Tentei fazer por substituição pois tem uma função composta. Chamei u =

mas eu não consegui fazer a substituição. Eu gostaria de resolver apenas dessa maneira, se eu puder... pois não adianta eu resolver de outro jeito se eu travei nessa última integral. Alguma luz? Grato desde já

-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Nov 24, 2013 20:10
por e8group » Dom Nov 24, 2013 20:10
Tome

,derivando-se :
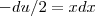
.
A nova integral fica

.
Agora tente por partes .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Danilo » Dom Nov 24, 2013 22:04
por Danilo » Dom Nov 24, 2013 22:04
santhiago escreveu:Tome

,derivando-se :
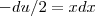
.
A nova integral fica

.
Agora tente por partes .
Santhiago, com a sua substuição deu certinho mas eu não consegui visualizar como vc substituiu!

e não dx (corrreto?). Por isso eu não consigo substituir (se eu não estiver errado) aí eu travo!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Seg Nov 25, 2013 11:24
por e8group » Seg Nov 25, 2013 11:24
OK . Primeiro pense : Qual a relação entre

e

? Para responder esta pergunta , basta notar que
![x^3 = (-1)(-1)x \cdot x^2 = [(-1)x] (-x^2) x^3 = (-1)(-1)x \cdot x^2 = [(-1)x] (-x^2)](/latexrender/pictures/0e6758e9343fa23f717f126ba49b9f0a.png)
.
Além disso, se
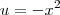
então
![du = [-x^2]' dx = (-2)x dx du = [-x^2]' dx = (-2)x dx](/latexrender/pictures/5fa04d49a13edb1c86fcdfb00e849fab.png)
e assim
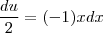
. Agora note que ,
![x^3 e^{-x^2} dx = [(-1)x] (-x^2) e^{(-x^2)} dx = (-x^2) \cdot e^{(-x^2)} [(-1)xdx] x^3 e^{-x^2} dx = [(-1)x] (-x^2) e^{(-x^2)} dx = (-x^2) \cdot e^{(-x^2)} [(-1)xdx]](/latexrender/pictures/cd48324ef45f2605ded6f027aeb1f9ca.png)
.
A expressão entre () pode ser substituída por

,já a expressão entre [] pode ser substituída por
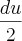
. Deste modo ,
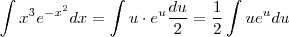
.
Peço desculpa ,no primeiro post errei contas . De qualquer forma espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida Resolução integral por partes!
por lucat28 » Sex Mar 18, 2011 14:47
- 2 Respostas
- 1708 Exibições
- Última mensagem por lucat28

Sex Mar 18, 2011 16:45
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Duvida na integração Por partes
por fabriel » Sáb Out 06, 2012 18:56
- 1 Respostas
- 1584 Exibições
- Última mensagem por MarceloFantini

Sáb Out 06, 2012 19:17
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4581 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por rita becher » Qua Jun 01, 2011 22:05
- 2 Respostas
- 2308 Exibições
- Última mensagem por rita becher

Qui Jun 02, 2011 10:30
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por rita becher » Qui Jun 02, 2011 00:20
- 4 Respostas
- 4000 Exibições
- Última mensagem por rita becher

Sáb Jun 04, 2011 13:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
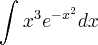
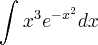

 mas eu não consegui fazer a substituição. Eu gostaria de resolver apenas dessa maneira, se eu puder... pois não adianta eu resolver de outro jeito se eu travei nessa última integral. Alguma luz? Grato desde já
mas eu não consegui fazer a substituição. Eu gostaria de resolver apenas dessa maneira, se eu puder... pois não adianta eu resolver de outro jeito se eu travei nessa última integral. Alguma luz? Grato desde já 


 ,derivando-se :
,derivando-se : 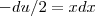 .
. .
. e não dx (corrreto?). Por isso eu não consigo substituir (se eu não estiver errado) aí eu travo!
e não dx (corrreto?). Por isso eu não consigo substituir (se eu não estiver errado) aí eu travo! e
e  ? Para responder esta pergunta , basta notar que
? Para responder esta pergunta , basta notar que ![x^3 = (-1)(-1)x \cdot x^2 = [(-1)x] (-x^2) x^3 = (-1)(-1)x \cdot x^2 = [(-1)x] (-x^2)](/latexrender/pictures/0e6758e9343fa23f717f126ba49b9f0a.png) .
. 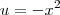 então
então![du = [-x^2]' dx = (-2)x dx du = [-x^2]' dx = (-2)x dx](/latexrender/pictures/5fa04d49a13edb1c86fcdfb00e849fab.png) e assim
e assim 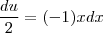 . Agora note que ,
. Agora note que , ![x^3 e^{-x^2} dx = [(-1)x] (-x^2) e^{(-x^2)} dx = (-x^2) \cdot e^{(-x^2)} [(-1)xdx] x^3 e^{-x^2} dx = [(-1)x] (-x^2) e^{(-x^2)} dx = (-x^2) \cdot e^{(-x^2)} [(-1)xdx]](/latexrender/pictures/cd48324ef45f2605ded6f027aeb1f9ca.png) .
. ,já a expressão entre [] pode ser substituída por
,já a expressão entre [] pode ser substituída por 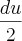 . Deste modo ,
. Deste modo , 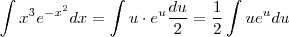 .
.