![\int_{}^{}\frac{dx}{\sqrt[]{{x}^{2}+{a}^{2}}} = ln(x + \sqrt[]{{x}^{2} + {a}^{2}}) + C \int_{}^{}\frac{dx}{\sqrt[]{{x}^{2}+{a}^{2}}} = ln(x + \sqrt[]{{x}^{2} + {a}^{2}}) + C](/latexrender/pictures/60f6baa45c752fc0e845aad793a1928b.png)


![\int_{}^{}\frac{dx}{\sqrt[]{{x}^{2}+{a}^{2}}} = ln(x + \sqrt[]{{x}^{2} + {a}^{2}}) + C \int_{}^{}\frac{dx}{\sqrt[]{{x}^{2}+{a}^{2}}} = ln(x + \sqrt[]{{x}^{2} + {a}^{2}}) + C](/latexrender/pictures/60f6baa45c752fc0e845aad793a1928b.png)

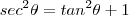 vemos que é possível realizar uma substituição trigonométrica
vemos que é possível realizar uma substituição trigonométrica  (desde que
(desde que  ) de modo obtermos outra integral mais simples . Se considerarmos
) de modo obtermos outra integral mais simples . Se considerarmos  , podemos sempre escrever
, podemos sempre escrever  sob a forma
sob a forma  para algum
para algum  em
em  . Segue-se que
. Segue-se que  (pois
(pois 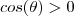 )
) ,
, 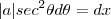 . Após esta substituição ,veja como a integral ficou mais simples de ser calculada :
. Após esta substituição ,veja como a integral ficou mais simples de ser calculada : 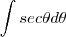

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)