UNICIDADE DO CONJUNTO VAZIO
Uma consequência direta do axioma da extensão é
Existe um único conjunto vazio.
Ora, se U e V são conjuntos distintos, deduz-se com o axioma da extensão que
 .
.Mas isto, por sua vez, implica
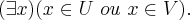
Logo, U e V distintos não podem ser ambos vazios.
Apenas em palavras:
Se dois conjuntos são diferentes então, pela contrapositiva do axioma da extensão, um deles possui um elemento que o outro não possui. Como os conjuntos em questão são vazios, não possuem elemento algum e, assim, somos obrigados a admitir que são iguais.

