Como eu resolvo o exercício?
Determine a equação da esfera que passa pelos pontos A=(2,3,-2), B=(1,0,-2) e C=(5,-1,-3) e possui centro no plano x-y+2z=-6
por anapmarinho » Dom Out 20, 2013 17:25
por e8group » Ter Out 22, 2013 20:22
o plano dado . E suponhamos que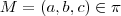 
seja o ponto médio da esfera .Ora ,se 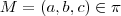, então suas coordenadas satisfaz a equação do plano que é : 
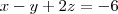. Logo , 
.
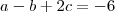. Assim , um ponto 
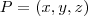pertence a esfera se, e somente se , 
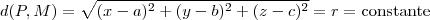, ou de forma equivalente 
.Por outro lado , ![r^2 = [d(A,M)]^2 = [d(B,M)]^2 ] = [d(C,M)]^2 ]](/latexrender/pictures/7afad1a5d9531973612cf465e10c8115.png "r^2 = [d(A,M)]^2 = [d(B,M)]^2 ] = [d(C,M)]^2 ]")
, ou seja ,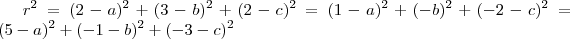 
. Através da igualdade 
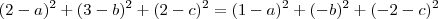e tendo em vista que os termos 
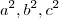em ambos lados da igualdade se cancelem , obteremos : 
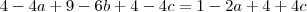e isolando uma das variáveis como por exemplo "b" , segue 
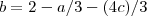, mas lembrando que 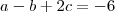, ou seja , 
,então ,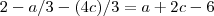
o que implica 
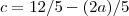, substituindo esta expressão em , obterá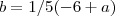 
. Encontramos então as variáveis 
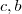em função de a . Para determinar 
. Basta substituir 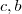em .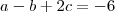 
Voltar para Geometria Analítica
por brunotorres101 » Qui Abr 09, 2015 00:27
por Eddie Hunter » Qua Abr 26, 2017 20:31
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
.
, 
e para 
, 
.
e 
, monte a função e substitua 
por 
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
