Estou relembrando agora o mundo das equações do segundo grau - dez anos após ter passado pelo colegial, e estou com dificuldade em resolver a seguinte equação:
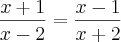
Eu cheguei no resultado correto, mas não sei se usei o método certo para alcançá-lo. Eis o que fiz:
MMC de x-2 e x+2 => (x-2)(x+2) --- Isso é certo?
x (x+2) + x + 2 = x (x-2) -1 (x-2) --- coloquei aqui todos os termos
x² + 2x + x + 2 = x² - 2x - x + 2 --- aqui alguns termos resolvidos (com a distributiva)
x² - x² + 2x + x + 2 = -2x - x + 2 --- passei o x² para o primeiro termo e o excluí (x² - x² = 0)
2x + x + 2 = -2x - x + 2
3x + 2 = -3x + 2 (os termos com x resolvidos)
3x + 3x = 2 - 2
6x = 0
x = 0 (resultado)
Eu cheguei nesse resultado resolvendo a equação meio que por "osmose", utilizando o único método que conheço. Eu fiz do jeito que "sei" e cheguei num resultado. Alguém pode me indicar alguma outra forma de se resolver essa equação ou a forma como resolvi é a única?



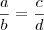 então é verdade também que
então é verdade também que  . Este é o famoso "multiplicar cruzado".
. Este é o famoso "multiplicar cruzado".

 .
.
 :
: