 por Man Utd » Dom Jul 14, 2013 23:45
por Man Utd » Dom Jul 14, 2013 23:45
Olá.

Pergunta: Existe uma regra prática para calcular a derivada de uma função módulo? Ex:|x²-9|, só conheço um método assim: transformando a função anterior em uma equivalente fica : y=sqrt(x²-9)^2 e assim deriva normalmente.
Grato a todos que ajudarem.

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por young_jedi » Seg Jul 15, 2013 00:02
por young_jedi » Seg Jul 15, 2013 00:02
Desconheço um método direto para fazer isto, talvez outro membro do fórum saiba algum, uma forma de fazer seria avaliar a função onde ela é positiva e negativa
no caso desta função ela é negativa para
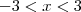
portanto pra este intervalo por causa do modulo ela seria o mesmo que

então a derivada nesse intervalo seria -2x
e para os pontos fora desse intervalo seria 2x
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Man Utd » Seg Jul 15, 2013 00:12
por Man Utd » Seg Jul 15, 2013 00:12
olá o wolfram dá outra resposta
http://www.wolframalpha.com/input/?i=de ... C2%B2-9%29 ,será que a derivada da função que o wolfram mostra é para os dois casos isto é quando a função é negativa e quando é positiva?
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por temujin » Seg Jul 15, 2013 14:05
por temujin » Seg Jul 15, 2013 14:05
Eu achei meio estranha esta resposta do Wolfram. Me parece que o que ele faz é primeiro aplicar o módulo e depois derivar (veja que o numerador e denominador se cancelam, qdo vc tira da raiz), o que daria a derivada para o caso em que é positiva. Mas se vc olhar o próprio gráfico que ele plota na resposta, ele mostra os dois casos: -2x se -3<x<3, 2x caso contrário.
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por young_jedi » Seg Jul 15, 2013 19:43
por young_jedi » Seg Jul 15, 2013 19:43
a resposta do wolfram vale para os dois casos, quando ele eleva ao quadrado e tira a raiz ele esta tomando o modulo
repare que para

e

o resultado de

sera um numero positivo, sendo dividido pelo seu modulo teremos como resultado 1, multiplicado por 2x é igual a 2x
agora caso tenhamos
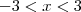
então

sera um numero negativo, dividido por seu modulo termos como resultado -1, que multiplicado por 2x é igual a -2x
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Man Utd » Seg Jul 15, 2013 23:55
por Man Utd » Seg Jul 15, 2013 23:55
muito obrigado young_jedi

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida (derivada e função modular)
 por Man Utd » Sáb Jun 15, 2013 11:03
por Man Utd » Sáb Jun 15, 2013 11:03
- 5 Respostas
- 7669 Exibições
- Última mensagem por LuizAquino

Dom Jun 16, 2013 11:24
Cálculo: Limites, Derivadas e Integrais
-
- Funçao modular
por Fiel8 » Sex Jul 10, 2009 19:25
- 1 Respostas
- 2616 Exibições
- Última mensagem por Molina

Sex Jul 10, 2009 21:50
Funções
-
- Função Modular
 por geriane » Sáb Abr 03, 2010 21:32
por geriane » Sáb Abr 03, 2010 21:32
- 3 Respostas
- 3114 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 12:57
Funções
-
- Funçao modular
 por Skcedas » Qua Mai 26, 2010 19:29
por Skcedas » Qua Mai 26, 2010 19:29
- 6 Respostas
- 5367 Exibições
- Última mensagem por netlopes

Ter Jun 08, 2010 18:11
Funções
-
- Função Modular
 por DanieldeLucena » Seg Set 20, 2010 18:03
por DanieldeLucena » Seg Set 20, 2010 18:03
- 1 Respostas
- 2244 Exibições
- Última mensagem por MarceloFantini

Seg Set 20, 2010 19:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






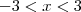




 e
e 
 sera um numero positivo, sendo dividido pelo seu modulo teremos como resultado 1, multiplicado por 2x é igual a 2x
sera um numero positivo, sendo dividido pelo seu modulo teremos como resultado 1, multiplicado por 2x é igual a 2x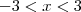 então
então  sera um numero negativo, dividido por seu modulo termos como resultado -1, que multiplicado por 2x é igual a -2x
sera um numero negativo, dividido por seu modulo termos como resultado -1, que multiplicado por 2x é igual a -2x



 .
.



