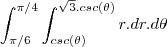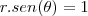![\int_{1}^{\sqrt[2]{3}} \int_{1}^{x} dydx](/latexrender/pictures/9a012373252acfbf99eb31c56e1a324c.png "\int_{1}^{\sqrt[2]{3}} \int_{1}^{x} dydx")
O que já fiz: Desenhei em coordenadas cartesianas o gráfico. No gráfico, é fácil de se ver que em 'x', as coordenadas variam de 1 à raiz de três. O mesmo acontece em 'y' pois y = x. Assim, obtive um triângulo retângulo e facilmente pude calcular que a área desejada era de:
![A = 2 - \sqrt[]{3}](/latexrender/pictures/b20441e32ec4afa5bc59f7eca518ac22.png "A = 2 - \sqrt[]{3}")
Calculando a integral:
![\int_{1}^{\sqrt[]{3}} \int_{1}^{x} dydx](/latexrender/pictures/7e574505b7fed71d13ca5a9fc2437931.png "\int_{1}^{\sqrt[]{3}} \int_{1}^{x} dydx")
pelo modo convencional, também consegui o valor
. Porém, ao converter para coordenadas polares, não estou conseguindo obter o valor correto obtido pelas formas de cálculo anteriores. Meus parâmetros foram os seguintes:![\int_{\frac{\pi}{4}}^{\frac{\pi}{6}} \int_{\csc \theta}^{\sqrt[]{3} \csc \theta} dydx](/latexrender/pictures/b7e6afc6a411a064c9d8ff4e3f63ce3a.png "\int_{\frac{\pi}{4}}^{\frac{\pi}{6}} \int_{\csc \theta}^{\sqrt[]{3} \csc \theta} dydx")
O que há de errado nos intervalos de integração? Alguém pode ajudar por favor?
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)