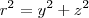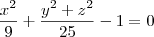por RobinhoOo22 » Qui Jun 27, 2013 21:10
por RobinhoOo22 » Qui Jun 27, 2013 21:10
1) Obtenha uma equação da superfície gerada pela rotação de cada curva em torno dos eixos
dados:
(a) geratriz: x^2/9+y^2/25-1= 0, z = 0; eixo: 0x;
(b) geratriz: 4x^2-y = 0, z = 0; eixo: 0y;
Bom gente, não consigo fazer esse exercicio, eu realmente não tenho ideia de como se faz ele, se alguém puder me ajudar

obrigado
-
RobinhoOo22
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jun 27, 2013 21:03
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por young_jedi » Sáb Jun 29, 2013 21:23
por young_jedi » Sáb Jun 29, 2013 21:23
no primeiro caso estaremos girando a curva em torno do eixo y, isso significa que se fizermos cortes no solido gerado, ao longo do eixo x, termos circunferências onde o raio de cada circunferencia depende de x, dado pela equação

mais r é dado por
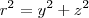
então temos que a equação do solidão sera
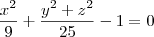
tente resolver o próximo e comente as duvidas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por RobinhoOo22 » Seg Jul 01, 2013 14:48
por RobinhoOo22 » Seg Jul 01, 2013 14:48
Entendi, muito obrigado, consegui fazer o outro também

Obrigado.
-
RobinhoOo22
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jun 27, 2013 21:03
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- obter o sistema linear de temperatura e obter na forma AX=B
por netochaves » Sáb Abr 06, 2013 18:20
- 0 Respostas
- 2360 Exibições
- Última mensagem por netochaves

Sáb Abr 06, 2013 18:20
Álgebra Linear
-
- obter o sistema linear de temperatura e obter na forma AX=B
por netochaves » Dom Abr 21, 2013 19:22
- 0 Respostas
- 1943 Exibições
- Última mensagem por netochaves

Dom Abr 21, 2013 19:22
Álgebra Linear
-
- (Quadricas) equação da superfície
por manuel_pato1 » Ter Dez 04, 2012 18:47
- 1 Respostas
- 4389 Exibições
- Última mensagem por young_jedi

Ter Dez 04, 2012 21:33
Geometria Analítica
-
- [Descobrir equação pela raiz]
por Mayra Luna » Qua Nov 21, 2012 17:59
- 2 Respostas
- 1466 Exibições
- Última mensagem por Mayra Luna

Qua Nov 21, 2012 21:10
Equações
-
- determinado pela equação cartesiana
por Neta Silva » Sex Mar 14, 2014 20:58
- 1 Respostas
- 1373 Exibições
- Última mensagem por Russman

Sex Mar 14, 2014 22:43
Introdução à Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 obrigado
obrigado
 obrigado
obrigado