por KleinIll » Qui Jun 20, 2013 17:52
por KleinIll » Qui Jun 20, 2013 17:52
Exercício: Uma carga elétrica é distribuída sobre uma placa
![R = \left[ \left(r,\theta) \right/ 0\leq\theta\leq\frac{\pi}{4}; 1\leq r\leq 2 \right] R = \left[ \left(r,\theta) \right/ 0\leq\theta\leq\frac{\pi}{4}; 1\leq r\leq 2 \right]](/latexrender/pictures/fa1dc8a87ad8afee5c25f16c218c8805.png)
. A densidade de carga é de
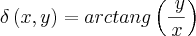
(medida em Coulombs por metro quadrado). Qual é a carga total da placa?
Sendo

e

Montei a integral dessa forma:

Porém, não consigo resolver o problema devida a equação de densidade de carga elétrica, que é dada por arco-tangente.
Alguém pode ajudar?
Obrigado.
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por young_jedi » Qui Jun 20, 2013 22:05
por young_jedi » Qui Jun 20, 2013 22:05
amigo, nos temos que
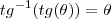
é so substituir na integral
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por KleinIll » Sex Jun 21, 2013 01:31
por KleinIll » Sex Jun 21, 2013 01:31
Obrigado. Eu só quero pedir mais uma coisa, caso não for incomodo, pode demonstrar ou apresentar os argumentos para que tg-¹(tgx) = x?
Edição: desconsidere, já esclareci.
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por Jhenrique » Sex Jun 21, 2013 17:37
por Jhenrique » Sex Jun 21, 2013 17:37
Tome como exemplo a equação y = x
Pode-se multiplicá-la por x, assim:
y/x = x/x
e terá:
y/x = 1
A ideia é análoga para y = f(x)
f?¹(y) = f?¹(f(x)) (a função inversa (f?¹) é aplicada na igualdade)
e resulta em:
f¹(y) = x
No seu caso, tg?¹(x) = arctg(x) = arco cuja tangente é x
fica assim:
arctg(tg(x)) = x
É como se as funções tg e arctg se cancelassem, da mesma forma quando adicionamos certo valor k em x e daí subtraimos esse mesmo valor k de x, ou seja, x + k - k = x.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por KleinIll » Sex Jun 21, 2013 19:18
por KleinIll » Sex Jun 21, 2013 19:18
Obrigado, Jhenrique.
Eu entendi quando pensei na própria função das funções dos arcos, que é retornar um ângulo a partir da relação trigonométrica correspondente, ou seja, se seno de 30º é 1/2, arcoseno de 1/2 é 30º.
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por Jhenrique » Sex Jun 21, 2013 22:46
por Jhenrique » Sex Jun 21, 2013 22:46
Exatamente!

Vc pega o caminho da ida e daí em seguida o da volta...
no final das contas vc não sai do lugar... xD
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por KleinIll » Sáb Jun 22, 2013 03:22
por KleinIll » Sáb Jun 22, 2013 03:22
huahuahuahuahuahuahuahua vdd xD
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral dupla
por DanielFerreira » Sex Mar 16, 2012 23:56
- 2 Respostas
- 2862 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 17, 2012 19:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 2
por DanielFerreira » Dom Mar 18, 2012 12:44
- 5 Respostas
- 4132 Exibições
- Última mensagem por DanielFerreira

Sex Mar 23, 2012 22:34
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 4
 por DanielFerreira » Sex Abr 06, 2012 19:49
por DanielFerreira » Sex Abr 06, 2012 19:49
- 4 Respostas
- 3117 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 21:05
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 5
por DanielFerreira » Sex Abr 06, 2012 20:00
- 2 Respostas
- 1903 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 20:16
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 6
 por DanielFerreira » Sáb Abr 14, 2012 22:54
por DanielFerreira » Sáb Abr 14, 2012 22:54
- 1 Respostas
- 1621 Exibições
- Última mensagem por LuizAquino

Dom Abr 15, 2012 23:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![R = \left[ \left(r,\theta) \right/ 0\leq\theta\leq\frac{\pi}{4}; 1\leq r\leq 2 \right] R = \left[ \left(r,\theta) \right/ 0\leq\theta\leq\frac{\pi}{4}; 1\leq r\leq 2 \right]](/latexrender/pictures/fa1dc8a87ad8afee5c25f16c218c8805.png) . A densidade de carga é de
. A densidade de carga é de 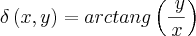 (medida em Coulombs por metro quadrado). Qual é a carga total da placa?
(medida em Coulombs por metro quadrado). Qual é a carga total da placa? e
e