 por netolucen4 » Sex Jun 21, 2013 05:26
por netolucen4 » Sex Jun 21, 2013 05:26
Em uma P.A

Onde

e
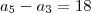
,
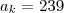
, então k é igual a quanto ?
Na formula para do

temo isso não é:
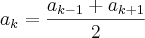
mas como encontrar o k ?
Essa eu não compreendi

só sei isso com esse k :(


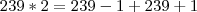
No caso o

é o último número, o n é a quantidade de termos da P.A, o

seria a media aritmética entre o antecedente e o consequente...
e o k seria o que ?
Estou totalmente fora do rumo nos pensamentos... alguém pode me dar uma ajuda do caminho? Agradeço desde já por a atenção de quem se der o trabalho de ajudar, muito obrigado mesmo ...
Editado pela última vez por
netolucen4 em Sex Jun 21, 2013 23:29, em um total de 2 vezes.
-
netolucen4
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jun 21, 2013 04:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Sex Jun 21, 2013 21:10
por young_jedi » Sex Jun 21, 2013 21:10
os temors de uma PA são dados por

onde r é razão da PA, isso você com certeza sabe
aplique isso para os termos a3 e a5 e calcule e a diferença entre eles como foi dado no enunciado, com isso você encontrara r e depois achar ak é tranquilo, se tiver duidas comente
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por netolucen4 » Sex Jun 21, 2013 22:28
por netolucen4 » Sex Jun 21, 2013 22:28
-
netolucen4
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jun 21, 2013 04:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Sex Jun 21, 2013 23:05
por young_jedi » Sex Jun 21, 2013 23:05
na verdade você tem que a5-a3 é igual a 14 e a2 igual a 18, você se confundiu na hora de substituir.
após corrigir e encontrar o r utilize


-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por netolucen4 » Sex Jun 21, 2013 23:55
por netolucen4 » Sex Jun 21, 2013 23:55
vou tentar .-.
-
netolucen4
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jun 21, 2013 04:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por netolucen4 » Sex Jun 21, 2013 23:57
por netolucen4 » Sex Jun 21, 2013 23:57
Não '-' confundi não a questão diz que a5-a3 é igual a 18 e a2 igual a 14

com as orientações que você me passou (que agradeço muito, muito, muito mesmo) encontrei o valor de 27 para K ...
-
netolucen4
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jun 21, 2013 04:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Sáb Jun 22, 2013 11:06
por young_jedi » Sáb Jun 22, 2013 11:06
Esta certo é isso mesmo!!!
k=27
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por netolucen4 » Sáb Jun 22, 2013 16:08
por netolucen4 » Sáb Jun 22, 2013 16:08
Muito obrigado por a paciência e mostrar o caminho para resolver a questão Young
Agradeço muito mesmo...
-
netolucen4
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jun 21, 2013 04:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Progressões aritméticas
por Alessandrasouza » Sex Mai 14, 2010 15:44
- 3 Respostas
- 2060 Exibições
- Última mensagem por Cleyson007

Sáb Mai 15, 2010 10:41
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Sáb Abr 07, 2012 01:13
- 2 Respostas
- 1301 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 07, 2012 01:31
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Dom Abr 08, 2012 21:10
- 2 Respostas
- 1623 Exibições
- Última mensagem por Anderson Alves

Qui Abr 12, 2012 22:41
Progressões
-
- Progressões Aritméticas
por Anderson Alves » Sáb Abr 14, 2012 13:42
- 1 Respostas
- 1662 Exibições
- Última mensagem por Lucio Carvalho

Sáb Abr 14, 2012 16:46
Progressões
-
- Progressões Aritméticas
por MarinaM » Dom Abr 15, 2012 00:24
- 2 Respostas
- 1816 Exibições
- Última mensagem por DanielFerreira

Dom Abr 15, 2012 19:56
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 e
e 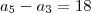 ,
, 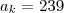 , então k é igual a quanto ?
, então k é igual a quanto ? temo isso não é:
temo isso não é: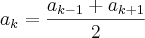



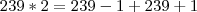
 é o último número, o n é a quantidade de termos da P.A, o
é o último número, o n é a quantidade de termos da P.A, o  seria a media aritmética entre o antecedente e o consequente...
seria a media aritmética entre o antecedente e o consequente...







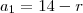
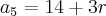
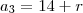
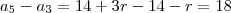









 , avisa que eu resolvo.
, avisa que eu resolvo.

