Dizemos que uma matriz A é simétrica se A^t = A e que A é antissimétrica se
At = -A. Mostre que
a. Se Amxn é uma matriz qualquer, então as matrizes Bnxn = A^t.A e Cmm = AA^t
são simétricas;
b. Se A é uma matriz quadrada de ordem n, então as matrizes B = 1/2(A+A^t)
e C = 1/2 (A - At) são, respectivamente, simétrica e antissimétrica;
c. Usando o item anterior, mostre que toda matriz pode ser escrita de forma única
como soma de uma matriz simétrica com uma antissimétrica;
d. Mostre que a única matriz que é, simultaneamente, simétrica e antissimétrica é a
matriz nula.
passo a passo em gente, valeu
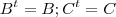.Para isto,note que : ![[A^t\cdot A]_{ij} = \sum_{k=1}^{n}[A^t]_{ik}[A]_{kj}](/latexrender/pictures/f108168f9d4df5673530f4f462b6b77f.png "[A^t\cdot A]_{ij} = \sum_{k=1}^{n}[A^t]_{ik}[A]_{kj}")
para todo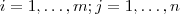
. Observando , ![[A^t]_{ik}[A]_{kj} = [A]_{ki}[A^t]_{jk}](/latexrender/pictures/660fa1091567d5c3807c75893228054b.png "[A^t]_{ik}[A]_{kj} = [A]_{ki}[A^t]_{jk}")
e como produtos de números são comutativos ,você pode concluir que ![[A]_{ki}[A^t]_{jk} = [A^t]_{jk} \cdot [A]_{ki}](/latexrender/pictures/31a67968d4ed6e8bf773379b07d93225.png "[A]_{ki}[A^t]_{jk} = [A^t]_{jk} \cdot [A]_{ki}")
.Logo , ![\sum_{k=1}^{n}[A^t]_{ik}[A]_{kj} = \sum_{k=1}^{n}[A^t]_{jk} \cdot [A]_{ki} = [B]_{ji}](/latexrender/pictures/33b2a968c89c731ca3bbf51df6a69715.png "\sum_{k=1}^{n}[A^t]_{ik}[A]_{kj} = \sum_{k=1}^{n}[A^t]_{jk} \cdot [A]_{ki} = [B]_{ji}")
para todo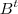
e na outra matriz ,evidencie 
e compare com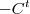 
. 
,respectivamente ,o conjunto das matrizes simétricas e anti-simétricas .Basta mostra que 
. Onde : 
é o vetor nulo do conjunto das matrizes 
.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.