Boa noite pessoal, estou com algumas dúvidas em relação a inequação modular com 2 ou mais módulos.
Dei uma pesquisada aqui pelo fórum e não encontrei nada que sanasse minha dúvida.
Vamos lá.
|x+4|<=|2x-6|
Resolvi assim
x+4 <= 2x - 6
-x <= -10 (-1)
x => 10
x+4 <= -2x + 6 (repare que não virei o sinal de desigualdade)
3x <= 2
x<= 2/3
Até aí tudo bem, está batendo direitinho com meu gabarito. Porém tem essa questão que é parecida.
|3+2x| < |4-x|
Tentei resolver do mesmo jeito!
3+2x < 4-x
3x<1
x<1/3
3+2x < -4 +x (Repare que TAMBÉM não virei o sinal de desigualdade)
x < -7
Porém no meu gabarito é x > -7, e eu ja revirei toda internet e não estou conseguindo entender por quê. Alguém pode me ajudar?


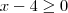

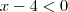

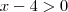
 ,neste caso a interseção é vazia .
,neste caso a interseção é vazia . 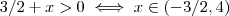
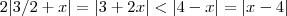 pelo caso (1) e (2) são iguais , como a interseção de (1) por (2) é vazia , a solução tem satisfazer (1) ou (2).Veja ,
pelo caso (1) e (2) são iguais , como a interseção de (1) por (2) é vazia , a solução tem satisfazer (1) ou (2).Veja , 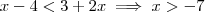 , logo
, logo 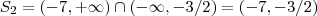 é um conjunto solução .Como no caso (3) a interseção é vazia ,só restou o última possibilidade .Segue então
é um conjunto solução .Como no caso (3) a interseção é vazia ,só restou o última possibilidade .Segue então  e portanto
e portanto 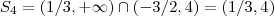 é o conjunto solução .Logo a reunião dos dois conjuntos obtidos acima é a solução da desigualdade .
é o conjunto solução .Logo a reunião dos dois conjuntos obtidos acima é a solução da desigualdade . .
.
 e
e 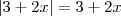 .Assim ,
.Assim ,  . Mas para
. Mas para 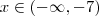 não temos :
não temos :  ,logo
,logo  .
.
 .
.
 :
: