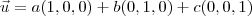por LucasSG » Qua Mai 29, 2013 17:47
por LucasSG » Qua Mai 29, 2013 17:47
9-26) Prove que as coordenadas de qualquer vetor

na base ortonormal B=(
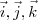
) são iguais aos produtos escalares de

por
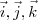
.
Pessoal, estou com uma duvida sobre como resolver esta questão. Poosso afirmar que
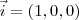
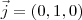
,
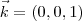
? Toda base ortonormal tem esta forma? Se sim eu consigo resolver, mas não quero afirmar isso sem ter certeza, porque no caso eu não estaria provando nada...

Muito Obrigado desde já!.
-
LucasSG
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 22, 2013 08:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por temujin » Qua Mai 29, 2013 18:08
por temujin » Qua Mai 29, 2013 18:08
Uma base é ortogonal se 2 vetores quaisquer do conjunto são ortogonais. E se eles tiverem norma unitária, a base é ortonormal. Esta em particular, a base canônica, é ortonormal, mas não é a única. Qualquer conjunto com 2 vetores L.I., com norma unitária, é ortonormal.
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por LucasSG » Qui Mai 30, 2013 16:24
por LucasSG » Qui Mai 30, 2013 16:24
Sim, entendi, então como eu poderia prosseguir para provar?, o enunciado diz que u=(u.i).i+(u.j).j+(u.k).k, como eu mostro que isso é verdade?
-
LucasSG
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 22, 2013 08:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por temujin » Qui Mai 30, 2013 23:12
por temujin » Qui Mai 30, 2013 23:12
Sejam

.
Podemos escrever o vetor
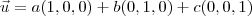
Esta é a expressão dos produtos escalares:



-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica] Base Ortonormal
por Pessoa Estranha » Seg Nov 04, 2013 22:18
- 0 Respostas
- 2104 Exibições
- Última mensagem por Pessoa Estranha

Seg Nov 04, 2013 22:18
Geometria Analítica
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4948 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- [Subconjunto de R^3]Equação Geral e Base Ortonormal de W.
por guisaulo » Ter Nov 27, 2012 21:42
- 2 Respostas
- 2304 Exibições
- Última mensagem por guisaulo

Qua Nov 28, 2012 12:03
Álgebra Linear
-
- [Gram Schimdt] achar base ortonormal
por Ge_dutra » Qua Jan 30, 2013 11:25
- 1 Respostas
- 1734 Exibições
- Última mensagem por young_jedi

Qui Jan 31, 2013 15:18
Álgebra Linear
-
- Produto escalar
por Carolziiinhaaah » Seg Mar 07, 2011 12:18
- 6 Respostas
- 4488 Exibições
- Última mensagem por Carolziiinhaaah

Seg Mar 07, 2011 19:25
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 na base ortonormal B=(
na base ortonormal B=(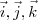 ) são iguais aos produtos escalares de
) são iguais aos produtos escalares de  por
por 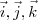 .
.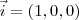
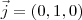 ,
, 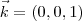 ? Toda base ortonormal tem esta forma? Se sim eu consigo resolver, mas não quero afirmar isso sem ter certeza, porque no caso eu não estaria provando nada...
? Toda base ortonormal tem esta forma? Se sim eu consigo resolver, mas não quero afirmar isso sem ter certeza, porque no caso eu não estaria provando nada... 



 .
.