Estou resolvendo uma lista de cálculo e gostaria de uma ajuda de vocês. Como sou da área de biológicas está sendo um pouco complicado relembrar alguns conceitos. Duas questões em específico tem me tirado o sono (hehe!), já tentei resolver algumas vezes mas sempre empaco em algum lugar. Uma delas é a seguinte:
O enunciado quer que se encontre as constantes da função, de modo que:
1.

Eu tentei resolver primeiramente tirando a constante b e colocando para fora, e em seguida multiplicando pelo conjugado
 , chegando ao seguinte:
, chegando ao seguinte: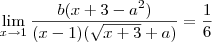
Mas depois disso não consigo chegar ao ponto de conseguir um sistema para resolver para "a" e "b", nem consigo tirar o (x-1) que está zerando o denominador.
Please, help!


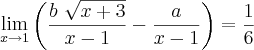

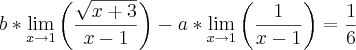


![{lim}_{x\rightarrow1}=\frac{b.\sqrt[]{x+3}-a}{x-1}={lim}_{x\rightarrow1}=\frac{b.\sqrt[]{x+3}-a}{x-1}.\frac{b.\sqrt[]{x+3}+a}{b.\sqrt[]{x+3}+a} {lim}_{x\rightarrow1}=\frac{b.\sqrt[]{x+3}-a}{x-1}={lim}_{x\rightarrow1}=\frac{b.\sqrt[]{x+3}-a}{x-1}.\frac{b.\sqrt[]{x+3}+a}{b.\sqrt[]{x+3}+a}](/latexrender/pictures/de34a208a34b967801a8074044cc1bb7.png)
![{lim}_{x\rightarrow1}=\frac{{b}^{2}(x+3)-{a}^{2}}{(x-1)(b.\sqrt[]{x+3}+a)} {lim}_{x\rightarrow1}=\frac{{b}^{2}(x+3)-{a}^{2}}{(x-1)(b.\sqrt[]{x+3}+a)}](/latexrender/pictures/77a4a5b85f8e883c7c0d99d2d228e2fb.png)
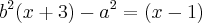
![b.\sqrt[]{1+3}+a=6 b.\sqrt[]{1+3}+a=6](/latexrender/pictures/58e72b82089987934394b8b725b46ab5.png)







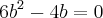
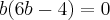

 , mas pela resposta encontrada esse raciocínio e´ errado. Será que você poderia explicar?
, mas pela resposta encontrada esse raciocínio e´ errado. Será que você poderia explicar?![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)