questão: Se A é um conjunto com 3 elementos e B um conjunto com 11elementos, quantas funções
existe ? Quantas delas são injetivas?
por Victor Gabriel » Qui Mai 09, 2013 19:21
existe ? Quantas delas são injetivas?
por brunoiria » Sex Mai 10, 2013 01:14
com elementos x e o conjunto 
com elementos y. Isto é:
de em que relaciona cada elemento x em , um único elemento y = f (x) em (de uma olhada em livros de matemática, tipo do iezzi ou do elon)
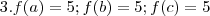
maneiras de expressar a função 
. 
por Victor Gabriel » Sex Mai 10, 2013 02:19
é uma correspondência que a cada elemento a de A associa um único elemento de B, denotando por f(a). , as injetivas são 
.Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
zig escreveu:
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.