 por arthurvct » Qua Abr 24, 2013 15:36
por arthurvct » Qua Abr 24, 2013 15:36
Prove que se

, então

ou vetor u=0
-
arthurvct
-
 por e8group » Sex Abr 26, 2013 18:18
por e8group » Sex Abr 26, 2013 18:18
Tente pensar assim :
Definimos
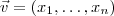
.Logo , por definição de produto de um escalar por um vetor ,temos :
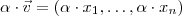
. Assim ,
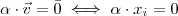
para cada
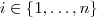
.Note que

e

são números ,e portanto
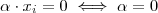
ou

.
Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sáb Mai 18, 2013 13:12
por e8group » Sáb Mai 18, 2013 13:12
Estar um pouco tarde ,mas vale apena compartilhar outra solução que segue de alguns axiomas do espaço vetorial .
Sejam
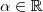
e

vetor do espaço vetorial

.
Consideremos dois casos :
(i)

(ii)
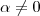
.
Prova :
![(i) \implies 0\cdot u = (0+0)u \overset{(b_3)}{=} 0\cdot u + 0\cdot u \implies 0\cdot u + (-0\cdot u) = (0\cdot u + 0\cdot u ) -0\cdot u 0 \overset{(a_2)}{=} [0\cdot u + (-0\cdot u)] + 0\cdot u \overset{(a_4)}{\implies} 0_V = 0_V + 0\cdot u \overset{(a_3)}{=} 0 \cdot u (i) \implies 0\cdot u = (0+0)u \overset{(b_3)}{=} 0\cdot u + 0\cdot u \implies 0\cdot u + (-0\cdot u) = (0\cdot u + 0\cdot u ) -0\cdot u 0 \overset{(a_2)}{=} [0\cdot u + (-0\cdot u)] + 0\cdot u \overset{(a_4)}{\implies} 0_V = 0_V + 0\cdot u \overset{(a_3)}{=} 0 \cdot u](/latexrender/pictures/e68a543dadfa2e8a87490dd68e043066.png)

.Assim ,
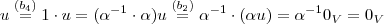
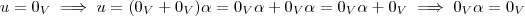
Onde :
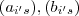
são os axiomas do espaço vetorial que não vou citar-los aqui e

vetor nulo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão de reta! Me ajudem!
por arthurvct » Ter Mai 21, 2013 14:39
- 3 Respostas
- 3008 Exibições
- Última mensagem por arthurvct

Sáb Mai 25, 2013 23:01
Geometria Analítica
-
- Por favor me ajudem Questão deN° de habitantes
por Rodrigopc1 » Seg Out 19, 2009 22:31
- 1 Respostas
- 2831 Exibições
- Última mensagem por Rodrigopc1

Seg Out 19, 2009 22:33
Sistemas de Equações
-
- me ajudem! questão cespe raciocínio
por leandro moraes » Qui Jun 10, 2010 08:49
- 0 Respostas
- 1211 Exibições
- Última mensagem por leandro moraes

Qui Jun 10, 2010 08:49
Estatística
-
- me ajudem com essa questao por favor!
por Anderson POntes » Ter Jul 13, 2010 10:55
- 1 Respostas
- 2241 Exibições
- Última mensagem por Tom

Ter Jul 13, 2010 13:08
Estatística
-
- questão concurso (cespe) ajudem!
por leandro moraes » Seg Jun 13, 2011 12:54
- 0 Respostas
- 1009 Exibições
- Última mensagem por leandro moraes

Seg Jun 13, 2011 12:54
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , então
, então  ou vetor u=0
ou vetor u=0
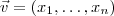 .Logo , por definição de produto de um escalar por um vetor ,temos :
.Logo , por definição de produto de um escalar por um vetor ,temos : 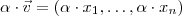 . Assim ,
. Assim , 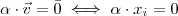 para cada
para cada 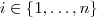 .Note que
.Note que  e
e  são números ,e portanto
são números ,e portanto 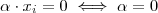 ou
ou 

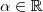 e
e  vetor do espaço vetorial
vetor do espaço vetorial  .
.
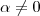 .
. ![(i) \implies 0\cdot u = (0+0)u \overset{(b_3)}{=} 0\cdot u + 0\cdot u \implies 0\cdot u + (-0\cdot u) = (0\cdot u + 0\cdot u ) -0\cdot u 0 \overset{(a_2)}{=} [0\cdot u + (-0\cdot u)] + 0\cdot u \overset{(a_4)}{\implies} 0_V = 0_V + 0\cdot u \overset{(a_3)}{=} 0 \cdot u (i) \implies 0\cdot u = (0+0)u \overset{(b_3)}{=} 0\cdot u + 0\cdot u \implies 0\cdot u + (-0\cdot u) = (0\cdot u + 0\cdot u ) -0\cdot u 0 \overset{(a_2)}{=} [0\cdot u + (-0\cdot u)] + 0\cdot u \overset{(a_4)}{\implies} 0_V = 0_V + 0\cdot u \overset{(a_3)}{=} 0 \cdot u](/latexrender/pictures/e68a543dadfa2e8a87490dd68e043066.png)
 .Assim ,
.Assim , 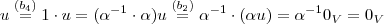
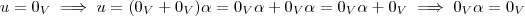
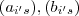 são os axiomas do espaço vetorial que não vou citar-los aqui e
são os axiomas do espaço vetorial que não vou citar-los aqui e  vetor nulo .
vetor nulo .


 , avisa que eu resolvo.
, avisa que eu resolvo.

