 por pedro30 » Sáb Abr 20, 2013 12:55
por pedro30 » Sáb Abr 20, 2013 12:55
Estou tentando resolver este exercício e não sei como começar, então se alguém puder me ajudar!!!
Comprove que as hipóteses do teorema de Rolle estão satisfeitas pela função dada no intervalo
indicado. Ache, um valor adequado de c que satisfaça a conclusão do teorema de Rolle.
a) f(x) = x² - 4x + 3; [1, 3]
b) f(x) = sen (2x); [ 0, 1/2 pi]
-
pedro30
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Abr 20, 2013 12:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por e8group » Sáb Abr 20, 2013 14:01
por e8group » Sáb Abr 20, 2013 14:01
Note que

é contínua em
![[1,3] [1,3]](/latexrender/pictures/689e1b934020b6eb3917c155d94a9a0f.png)
e diferenciável em
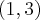
.Além disso,

.Assim ,pelo de
Teorema de Rolle,existe algum número

em
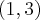
tal que
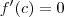
.De fato ,
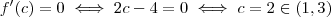
.
Proceda da mesma forma p/ a outra função .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema de Rolle
por Mel92 » Sex Nov 23, 2012 23:57
- 5 Respostas
- 3400 Exibições
- Última mensagem por Mel92

Sáb Nov 24, 2012 18:44
Cálculo: Limites, Derivadas e Integrais
-
- Problema com o teorema de Rolle
por Rebecafer » Qua Ago 14, 2013 15:38
- 6 Respostas
- 2392 Exibições
- Última mensagem por Rebecafer

Qui Ago 15, 2013 23:57
Equações
-
- Derivada teorema de Rolle
 por juflamanto » Sáb Out 10, 2015 21:24
por juflamanto » Sáb Out 10, 2015 21:24
- 1 Respostas
- 1203 Exibições
- Última mensagem por adauto martins

Sex Out 30, 2015 12:24
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida : Teorema de Pitagoras
por Mariana111 » Seg Out 26, 2009 17:30
- 5 Respostas
- 3966 Exibições
- Última mensagem por Mariana111

Seg Out 26, 2009 21:08
Geometria Analítica
-
- Duvida em teorema de pitagoras
 por tadeutato » Sáb Abr 30, 2011 15:37
por tadeutato » Sáb Abr 30, 2011 15:37
- 1 Respostas
- 1105 Exibições
- Última mensagem por FilipeCaceres

Sáb Abr 30, 2011 15:51
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 é contínua em
é contínua em ![[1,3] [1,3]](/latexrender/pictures/689e1b934020b6eb3917c155d94a9a0f.png) e diferenciável em
e diferenciável em 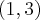 .Além disso,
.Além disso,  .Assim ,pelo de
.Assim ,pelo de em
em 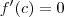 .De fato ,
.De fato , 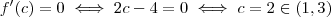 .
. 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.