 por timoteo » Qua Abr 10, 2013 13:02
por timoteo » Qua Abr 10, 2013 13:02
Olá está questão foi da UFPE-2013 questão 06. O resultado não bate com os cálculos mostrados!
Questão:
Uma compra em uma loja da Internet custa 1250 libras esterlinas, incluindo os custos de envio. Para o pagamento no Brasil, o valor deve ser inicialmente convertido em dólares e, em seguida, o valor em dólares é convertido para reais. Além disso, paga-se 60% de imposto de importação à Receita Federal e 6,38% de IOF para pagamento no cartão de crédito. Se uma libra esterlina custa 1,6 dólares e um dólar custa 2 reais, calcule o valor a ser pago, em reais, e indique a soma de seus dígitos.
Resposta: 27
É a próxima conta que não bate, vejam:
Solução:
O valor a ser pago será de reais 1250.1,6.2.1,0638 = 6808,32 reais. --> Este valor não bate, quando calculo acho: 4255,2 reais!
Qual o calculo correto?
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por DanielFerreira » Ter Abr 16, 2013 15:16
por DanielFerreira » Ter Abr 16, 2013 15:16
Timoteo,
discordo da solução apresentada. Vou postar minha resolução e vamos aguardar os comentários dos outros colegas!
Conversão:
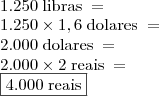 Imposto
Imposto:
 IOF
IOF:

Portanto,
R$ 4.000,00 + R$ 2.400,00 + R$ 255,20 =
R$ 6.655,20 Até o momento, não consegui 'desvendar' como apareceu aquele
1,0638 na multiplicação!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por timoteo » Ter Abr 16, 2013 19:06
por timoteo » Ter Abr 16, 2013 19:06
Olá Dan, eu também não consigo entender esta resposta.
Porém, foi-me dada uma resolução que em parte compreendi e em parte não. Esta resposta foi apresentada em outro site que participo, o tutorbrasil.
Resolução: por ttbr96 » Qui 11 Abr, 2013 17:50
conversão de libra para real: 1250 x 1,6 x 2 = 4000
valor do IOF: 4000 x 0,0638 = 255,20
valor a ser pago antes do imposto de importação: 4000 + 255,20 = 4255,20
valor do imposto de importação: 4255,20 x 0,6 = 2553,12
valor a ser pago: 4255,0 + 2553,12 = 6808,32
ou
1250 x 1,6 x 2 x 1,0638 x 1,6 = 6808,32
soma dos dígitos: 6 + 8 + 0 + 8 + 3 + 2 = 27.
Até antes do ou eu concordo; eu como amador faria isso. Porém, quando chega abaixo do ou eu não entendo por que apareceu duas vezes o valor de 1,6, sendo que o enunciado e a própria resolução inicial dele não aparece.
Se você entender me explique!
Obrigado pela colaboração!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por DanielFerreira » Ter Abr 16, 2013 21:22
por DanielFerreira » Ter Abr 16, 2013 21:22
Olá Timoteo,
boa noite!
Agora percebo que me equivoquei ao não calcular o imposto 'embutido' na soma (conversão + IOF). Portanto, R$ 6.808,32 valor correto!
No entanto, ainda não entendi o fato que está a indagar. Certamente, há algum 'macete' envolvido que não conhecemos.
Talvez, algum colega daqui (Ajuda Matemática) possa nos ajudar a compreender melhor a segunda resolução.
Até!!
Att,
Daniel.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- a sua resposta!!
por weverton » Seg Jul 12, 2010 18:44
- 1 Respostas
- 1374 Exibições
- Última mensagem por weverton

Seg Jul 12, 2010 19:22
Progressões
-
- Nao comsegui axa a resposta ...
por jean » Sáb Nov 29, 2008 17:44
- 2 Respostas
- 2025 Exibições
- Última mensagem por jean

Sáb Nov 29, 2008 21:45
Pedidos
-
- resposta urgente
por vinicius gouveia » Seg Dez 23, 2013 22:17
- 1 Respostas
- 1474 Exibições
- Última mensagem por young_jedi

Seg Dez 23, 2013 23:09
Conjuntos
-
- dúvida na resposta
por Anderson Claiton 77 » Dom Ago 23, 2015 12:41
- 1 Respostas
- 1359 Exibições
- Última mensagem por Matpas

Qui Ago 27, 2015 17:55
Funções
-
- PRECISO URGENTEMENTE DE RESPOSTA
por ems » Sex Fev 22, 2008 17:47
- 2 Respostas
- 3125 Exibições
- Última mensagem por ems

Sáb Fev 23, 2008 21:31
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


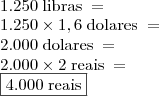





 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.