Tenho uma questão de um trabalho para resolver, mas não consegui de jeito nenhum.
admita que a distribuição de altura entre os jogadores de basquete é uma normal com desvio padrão 20 cm. sabe-se que 40 % desses jogadores tem mais de 2m de altura.
A- determine a média.
B- que percentagem dos jogadores tem menos de 1,80m de altura.
Agradeço a todos que puderem ajudar!!


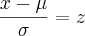
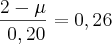
 ) = P(Z< -0,74)
) = P(Z< -0,74)

 .
.
 :
: