O zero não é máximo nem mínimo no exemplo, justamente pq a derivada não muda de sinal. O que caracteriza um ponto como um extremo (máx ou min) é a mudança de sinal. Por exemplo, compare duas funções

. Ambas tem o zero como ponto crítico, certo?
Mas se vc olhar pra derivada, no caso da
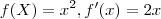
. Então, para valores negativos de x, f'(x) é negativa. Para valores positivos de x, f'I(x) é positiva. Ou seja, a função vem decrescendo pela esquerda, vira no zero e passa a crescer para valores à direita.
Agora veja o caso da

. Para valores negativos, f'(x) é positiva. No zero, ela é zero mesmo. E para valores positivos ela tb é positiva. Não há mudança de sinal.
Ser ponto crítico é condição necessária, mas não suficiente, para ser um extremo.


 é crescente se
é crescente se 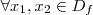 e
e  .Por outro lado
.Por outro lado 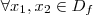 e
e  .Alternativamente ,
.Alternativamente , 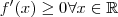 e
e  .
. 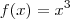 que é estritamente crescente pois
que é estritamente crescente pois 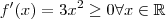 .Neste caso
.Neste caso  é ponto crítico da função ,mas 0 não é máximo e nem mínimo da função
é ponto crítico da função ,mas 0 não é máximo e nem mínimo da função 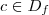 e
e 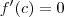 e se para algum
e se para algum 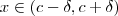 e
e  mudar de sinal ,então o ponto
mudar de sinal ,então o ponto  será máximo[ou mínimo] local .
será máximo[ou mínimo] local .
 . Ambas tem o zero como ponto crítico, certo?
. Ambas tem o zero como ponto crítico, certo?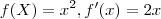 . Então, para valores negativos de x, f'(x) é negativa. Para valores positivos de x, f'I(x) é positiva. Ou seja, a função vem decrescendo pela esquerda, vira no zero e passa a crescer para valores à direita.
. Então, para valores negativos de x, f'(x) é negativa. Para valores positivos de x, f'I(x) é positiva. Ou seja, a função vem decrescendo pela esquerda, vira no zero e passa a crescer para valores à direita.  . Para valores negativos, f'(x) é positiva. No zero, ela é zero mesmo. E para valores positivos ela tb é positiva. Não há mudança de sinal.
. Para valores negativos, f'(x) é positiva. No zero, ela é zero mesmo. E para valores positivos ela tb é positiva. Não há mudança de sinal.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)