![\lim_{x->2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2}](/latexrender/pictures/9e328d21f2f24b18164967a6b92e3070.png "\lim_{x->2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2}")
, mas estou tendo problemas para utilizar a formula de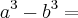 
(a-b)*(a^2+ab+b^2) pois eu pesquisei em outros locais mas eles resolvem apenas deixando a parte de baixo (x-2) como a de cima. Estou em duvida se posso resolver a parte de cima ao inves da parte de baixo e se qnd for "simplificar" eu devo sempre colocar a ![\sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png "\sqrt[3]{x}")
ou somente
para "a".Ou seja, devo resolver fazendo assim:
![\sqrt[3]{x}-\sqrt[3]{2}](/latexrender/pictures/5ff21f1fed38444f63a4e01c32543170.png "\sqrt[3]{x}-\sqrt[3]{2}")
=........ ou apenas assim 
=.....Nao sei se vcs entenderam a pergunta e peço desculpas se postei em local errado ou com tema incorreto. Grato desde ja
![x - 2 = (x^3)^{1/3} - (2^3)^{1/3} = (\sqrt[3]{x})^3 - (\sqrt[3]{2})^3](/latexrender/pictures/eec1f1f7da0f0770630cbef599a293a9.png "x - 2 = (x^3)^{1/3} - (2^3)^{1/3} = (\sqrt[3]{x})^3 - (\sqrt[3]{2})^3")
. 
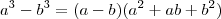.Substituindo-se ![a = \sqrt[3]{x}](/latexrender/pictures/fcb7438849ec4c127e7b09d293d32897.png "a = \sqrt[3]{x}")
e ![b = \sqrt[3]{2}](/latexrender/pictures/a90aa25ac8706f1f972723d12adfb9ed.png "b = \sqrt[3]{2}")
obtemos ![(\sqrt[3]{x})^3 - (\sqrt[3]{2})^3 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2)](/latexrender/pictures/979a77505951b5effaf8888254ad3c2a.png "(\sqrt[3]{x})^3 - (\sqrt[3]{2})^3 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2)")
. ![x - 2 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2)](/latexrender/pictures/43736e0f325424fa0e199739dd3236de.png "x - 2 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2)")
. 
.
: