 por Erick » Dom Mar 17, 2013 13:30
por Erick » Dom Mar 17, 2013 13:30
Estou tentando resolver o seguinte limite:
![\lim_{x->2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2} \lim_{x->2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2}](/latexrender/pictures/9e328d21f2f24b18164967a6b92e3070.png)
, mas estou tendo problemas para utilizar a formula de
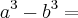
(a-b)*(a^2+ab+b^2) pois eu pesquisei em outros locais mas eles resolvem apenas deixando a parte de baixo (x-2) como a de cima. Estou em duvida se posso resolver a parte de cima ao inves da parte de baixo e se qnd for "simplificar" eu devo sempre colocar a
![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png)
ou somente

para "a".
Ou seja, devo resolver fazendo assim:
![\sqrt[3]{x}-\sqrt[3]{2} \sqrt[3]{x}-\sqrt[3]{2}](/latexrender/pictures/5ff21f1fed38444f63a4e01c32543170.png)
=........ ou apenas assim

=.....
Nao sei se vcs entenderam a pergunta e peço desculpas se postei em local errado ou com tema incorreto. Grato desde ja
-
Erick
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mar 17, 2013 13:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Dom Mar 17, 2013 14:32
por e8group » Dom Mar 17, 2013 14:32
Observe que
![x - 2 = (x^3)^{1/3} - (2^3)^{1/3} = (\sqrt[3]{x})^3 - (\sqrt[3]{2})^3 x - 2 = (x^3)^{1/3} - (2^3)^{1/3} = (\sqrt[3]{x})^3 - (\sqrt[3]{2})^3](/latexrender/pictures/eec1f1f7da0f0770630cbef599a293a9.png)
.
Sabemos que
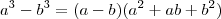
.Substituindo-se
![a = \sqrt[3]{x} a = \sqrt[3]{x}](/latexrender/pictures/fcb7438849ec4c127e7b09d293d32897.png)
e
![b = \sqrt[3]{2} b = \sqrt[3]{2}](/latexrender/pictures/a90aa25ac8706f1f972723d12adfb9ed.png)
obtemos
![(\sqrt[3]{x})^3 - (\sqrt[3]{2})^3 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2) (\sqrt[3]{x})^3 - (\sqrt[3]{2})^3 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2)](/latexrender/pictures/979a77505951b5effaf8888254ad3c2a.png)
.
Ou seja ,
![x - 2 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2) x - 2 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2)](/latexrender/pictures/43736e0f325424fa0e199739dd3236de.png)
.
Agora tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Erick » Dom Mar 17, 2013 14:42
por Erick » Dom Mar 17, 2013 14:42
Eu estava com exatamente esta duvida. Agr eu entendi, mt obrigado
-
Erick
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mar 17, 2013 13:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo I] Limites envolvendo raízes.
por Jefferson_mcz » Seg Mar 18, 2013 14:00
- 1 Respostas
- 1720 Exibições
- Última mensagem por young_jedi

Seg Mar 18, 2013 20:35
Cálculo: Limites, Derivadas e Integrais
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8121 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- [Radiciação] Raízes dentro de raízes
por mottasky » Ter Set 13, 2011 22:00
- 2 Respostas
- 2581 Exibições
- Última mensagem por mottasky

Qui Set 15, 2011 15:52
Álgebra Elementar
-
- Problema envolvendo função
por marianacarvalhops » Sáb Mai 02, 2009 17:46
- 1 Respostas
- 4424 Exibições
- Última mensagem por Marcampucio

Sáb Mai 02, 2009 18:27
Funções
-
- Problema envolvendo equação
por ana tereza » Qui Set 10, 2009 23:47
- 3 Respostas
- 5751 Exibições
- Última mensagem por gabrielMAT

Qua Out 19, 2011 16:49
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x->2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2} \lim_{x->2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2}](/latexrender/pictures/9e328d21f2f24b18164967a6b92e3070.png) , mas estou tendo problemas para utilizar a formula de
, mas estou tendo problemas para utilizar a formula de 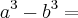 (a-b)*(a^2+ab+b^2) pois eu pesquisei em outros locais mas eles resolvem apenas deixando a parte de baixo (x-2) como a de cima. Estou em duvida se posso resolver a parte de cima ao inves da parte de baixo e se qnd for "simplificar" eu devo sempre colocar a
(a-b)*(a^2+ab+b^2) pois eu pesquisei em outros locais mas eles resolvem apenas deixando a parte de baixo (x-2) como a de cima. Estou em duvida se posso resolver a parte de cima ao inves da parte de baixo e se qnd for "simplificar" eu devo sempre colocar a ![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) ou somente
ou somente para "a".
para "a".![\sqrt[3]{x}-\sqrt[3]{2} \sqrt[3]{x}-\sqrt[3]{2}](/latexrender/pictures/5ff21f1fed38444f63a4e01c32543170.png) =........ ou apenas assim
=........ ou apenas assim  =.....
=.....

![x - 2 = (x^3)^{1/3} - (2^3)^{1/3} = (\sqrt[3]{x})^3 - (\sqrt[3]{2})^3 x - 2 = (x^3)^{1/3} - (2^3)^{1/3} = (\sqrt[3]{x})^3 - (\sqrt[3]{2})^3](/latexrender/pictures/eec1f1f7da0f0770630cbef599a293a9.png) .
. 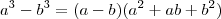 .Substituindo-se
.Substituindo-se ![a = \sqrt[3]{x} a = \sqrt[3]{x}](/latexrender/pictures/fcb7438849ec4c127e7b09d293d32897.png) e
e ![b = \sqrt[3]{2} b = \sqrt[3]{2}](/latexrender/pictures/a90aa25ac8706f1f972723d12adfb9ed.png) obtemos
obtemos ![(\sqrt[3]{x})^3 - (\sqrt[3]{2})^3 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2) (\sqrt[3]{x})^3 - (\sqrt[3]{2})^3 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2)](/latexrender/pictures/979a77505951b5effaf8888254ad3c2a.png) .
. ![x - 2 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2) x - 2 = (\sqrt[3]{x} - \sqrt[3]{2} )( [\sqrt[3]{x}]^2 + \sqrt[3]{x} \cdot \sqrt[3]{2} + (\sqrt[3]{2})^2)](/latexrender/pictures/43736e0f325424fa0e199739dd3236de.png) .
. 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
