 por e8group » Sex Mar 15, 2013 22:03
por e8group » Sex Mar 15, 2013 22:03
Faça a seguinte substituição ,

.Assim , quando

;logo ,
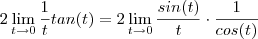
De
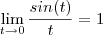
e
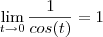
,obtemos

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglas16 » Sex Mar 15, 2013 23:13
por Douglas16 » Sex Mar 15, 2013 23:13
Valeu santhiago, mas gostaria de saber se você já encontrou a resolução na primeira observação da questão, ou fez mais de uma observação (tentativa) até concluir qual a forma correta para resolver?
Tipo, quero saber qual o raciocínio que você usou para começar a resolver o limite.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sáb Mar 16, 2013 00:07
por e8group » Sáb Mar 16, 2013 00:07
A observação que você tem que nota é que
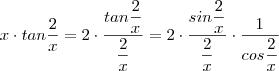
.
Para


muito grande (em módulo ) ,

se aproxima de zero .Por este motivo é conveniente a mudança de variável conforme postei acima ; logo ,o resultado do limite segue de imediato do limite fundamental trigonométrico e pelo fato que

quando

ou

quando

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglas16 » Sáb Mar 16, 2013 10:49
por Douglas16 » Sáb Mar 16, 2013 10:49
Então, minha pergunta foi mais para aprender como as outras pessoas se posicionam diante de uma questão assim.
Tipo, eu por exemplo muitas vezes, quando fui resolver um problema, procuro deixar de me focar em uma só possível forma de começar, para pensar em quantas formas eu puder encontrar e, assim avaliar qual é a melhor e correta forma de resolver a questão, só depois disso eu procuro colocar a "mão na massa". Por exemplo se pensei numa forma de resolver, primeiro desenvolver mentalmente a resolução para depois, caso ela aparentar nenhum erro de lógica, aí sim desenvolver no papel.
Foi isso que eu quis dizer como minha última dúvida.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Identidade Trigonometrica
por MERLAYNE » Ter Abr 24, 2012 19:40
- 4 Respostas
- 2453 Exibições
- Última mensagem por DanielFerreira

Ter Abr 24, 2012 20:12
Trigonometria
-
- [Trigonometria] Identidade trigonometrica
por Alvadorn » Sáb Ago 13, 2011 17:47
- 2 Respostas
- 1886 Exibições
- Última mensagem por Alvadorn

Sáb Ago 13, 2011 20:27
Trigonometria
-
- identidade trigonométrica fundamental
por zenildo » Qui Jun 27, 2013 20:21
- 1 Respostas
- 1479 Exibições
- Última mensagem por young_jedi

Sex Jun 28, 2013 11:22
Trigonometria
-
- [Limite] função trigonométrica
por rafaelbr91 » Ter Mar 27, 2012 17:51
- 2 Respostas
- 2163 Exibições
- Última mensagem por rafaelbr91

Ter Mar 27, 2012 18:43
Cálculo: Limites, Derivadas e Integrais
-
- Limite de uma função trigonométrica
por Douglas16 » Seg Mar 11, 2013 14:45
- 1 Respostas
- 1387 Exibições
- Última mensagem por Douglas16

Seg Mar 11, 2013 15:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
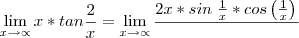

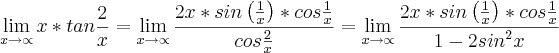
 do numerador, mas para isso eu tenho que expressar
do numerador, mas para isso eu tenho que expressar  em função de
em função de  .
.

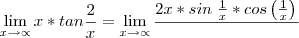

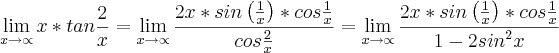
 do numerador, mas para isso eu tenho que expressar
do numerador, mas para isso eu tenho que expressar  em função de
em função de  .
.

 .Assim , quando
.Assim , quando  ;logo ,
;logo , 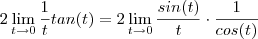
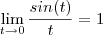 e
e 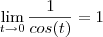 ,obtemos
,obtemos  .
.

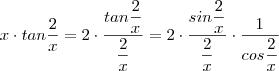 .
.
 muito grande (em módulo ) ,
muito grande (em módulo ) ,  se aproxima de zero .Por este motivo é conveniente a mudança de variável conforme postei acima ; logo ,o resultado do limite segue de imediato do limite fundamental trigonométrico e pelo fato que
se aproxima de zero .Por este motivo é conveniente a mudança de variável conforme postei acima ; logo ,o resultado do limite segue de imediato do limite fundamental trigonométrico e pelo fato que  quando
quando  ou
ou  quando
quando  .
.
