 por paulorobertoqf » Seg Mar 04, 2013 14:06
por paulorobertoqf » Seg Mar 04, 2013 14:06
Considere a função f(x), cujo gráfico é mostrado no anexo ''Gráfico''. Define-se g(x) pela seguinte expressão:

A expressão de g(x) para o intervalo

é:
A)

B)
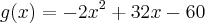
C)
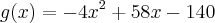
D)

E)

Calculei a área pelo gráfico fazendo (8-5)x12 e dividindo por 3, que deu 12, depois fiz a integral definida de 5 a 8 e várias das resposta dão 12, então não sei qual escolher.
A resposta correta é: B, mas não sei o porque.
- Anexos
-
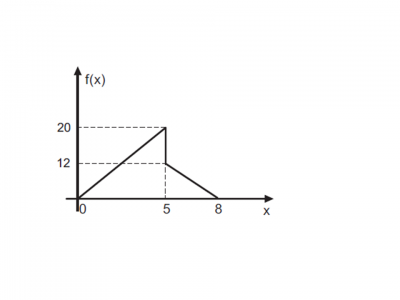
- Gráfico
-
paulorobertoqf
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 20, 2013 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Seg Mar 04, 2013 23:22
por young_jedi » Seg Mar 04, 2013 23:22
voce tem que
primeiro voce tem que parametrizar as duas reta da função para os dois intervalos
no primeiro intervalo

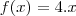
e para
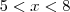

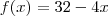
então a integral que voce quer fica
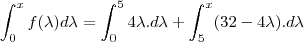
calcule a integral e comente qualquer duvida
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Gráfico.
por Josiebruno » Seg Out 18, 2010 18:47
- 3 Respostas
- 3142 Exibições
- Última mensagem por Josiebruno

Ter Out 19, 2010 12:24
Funções
-
- gráfico
por Andreza » Qui Nov 24, 2011 13:23
- 0 Respostas
- 1514 Exibições
- Última mensagem por Andreza

Qui Nov 24, 2011 13:23
Funções
-
- Grafico
por bruno ken taniwaki » Dom Fev 24, 2013 14:36
- 0 Respostas
- 1226 Exibições
- Última mensagem por bruno ken taniwaki

Dom Fev 24, 2013 14:36
Cálculo: Limites, Derivadas e Integrais
-
- gráfico
por Jhennyfer » Seg Mai 20, 2013 08:34
- 0 Respostas
- 1218 Exibições
- Última mensagem por Jhennyfer

Seg Mai 20, 2013 08:34
Funções
-
- Gráfico com f(x)=cos.x?
por Paulo Ricardo » Qua Ago 14, 2013 03:24
- 1 Respostas
- 1780 Exibições
- Última mensagem por Russman

Qua Ago 14, 2013 21:04
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 é:
é:
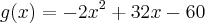
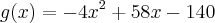





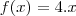
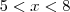

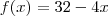
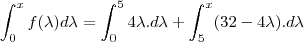


 .
.
 :
: