estou iniciando alguns exercícios de logaritmo, e não consigo resolver um aqui, se alguem puder me ajudar.
log de 0,000064 na base 5
eu faço até aqui:
log 5 64/10^6 => log 5 2^5 - log 5 10^6 => 5.log 5 2 - 6.log 5 10



nilcosta escreveu:estou iniciando alguns exercícios de logaritmo, e não consigo resolver um aqui, se alguem puder me ajudar.
log de 0,000064 na base 5
eu faço até aqui:
log 5 64/10^6 => log 5 2^5 - log 5 10^6 => 5.log 5 2 - 6.log 5 10
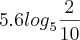


 = 30 (0 - 1) = 30(-1) = -30.
= 30 (0 - 1) = 30(-1) = -30.


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes