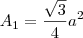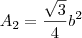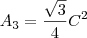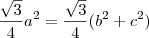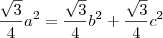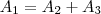por marlenit_a » Qua Jan 09, 2013 12:50
por marlenit_a » Qua Jan 09, 2013 12:50
1. Recorrendo a um programa de geometria dinâmica, desenhar um triângulo retângulo e sobre cada um dos seus lados construir um triângulo equilátero. Existe uma relação entre as áreas dos triângulos construídos. Estabelecer essa relação.
2. Mostrar analiticamente que as áreas dos triângulos equiláteros verificam a relação estabelecida na questão anterior.
-
marlenit_a
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jan 09, 2013 12:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Educação Básica
- Andamento: cursando
 por young_jedi » Qua Jan 09, 2013 20:24
por young_jedi » Qua Jan 09, 2013 20:24
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria
por ehrefundini » Ter Abr 22, 2008 16:53
- 3 Respostas
- 7325 Exibições
- Última mensagem por admin

Qui Mai 01, 2008 15:57
Pedidos de Materiais
-
- geometria 2
por ehrefundini » Qua Mai 07, 2008 10:35
- 1 Respostas
- 6037 Exibições
- Última mensagem por admin

Qua Mai 07, 2008 10:59
Pedidos de Materiais
-
- Geometria
por rybb » Ter Ago 25, 2009 07:48
- 1 Respostas
- 2872 Exibições
- Última mensagem por Elcioschin

Seg Out 05, 2009 22:41
Trigonometria
-
- Geometria - help me?
por rybb » Ter Ago 25, 2009 07:55
- 3 Respostas
- 7316 Exibições
- Última mensagem por Molina

Qua Ago 26, 2009 23:18
Geometria
-
- geometria
por cristina » Qui Nov 19, 2009 07:05
- 0 Respostas
- 2467 Exibições
- Última mensagem por cristina

Qui Nov 19, 2009 07:05
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.