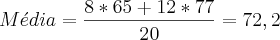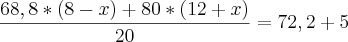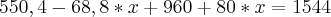Ola a todos, sou novo aqui e nao sei se o assunto esta na categoria certa. mas ai esta minha duvida sobre media aritmetica
Numa classe com vinte alunos, as notas do exame final podiam variar de 0 a 100 e a nota mínima para aprovação era 70. Realizado o exame, verificou-se que 8 alunos foram reprovados. A média aritmética das notas desses oito alunos foi 65, enquanto que a média dos aprovados foi 77. Após a divulgação dos resultados, o professor verificou que uma questão havia sido mal formulada e decidiu atribuir 5 pontos a mais para todos os alunos. Com essa decisão, a média dos aprovados passou a ser 80 e a dos reprovados 68,8.
a) Calcule a média aritmética das notas da classe toda antes da atribuição dos cinco pontos extras.
b) Com a atribuição dos cinco pontos extras, quantos alunos, inicialmente reprovados, atingiram nota para a aprovação?
RESOLUÇÃO: a) 72,2
b) 3
A primeira parte eu consegui vejam:
total alunos TA = 20
reprovados = 8,
logo aprovados A = 12
media dos reprovados MR = 65
media dos aprovados MA = 77
Soma das notas dos aprovados - SA
MA = SA / 12
SA = MA * 12
SA = 77 * 12
SA = 924
Soma das notas dos reprovados - SR
MR = SR / 8
SR = MR * 8
SR = 65 * 8
SR = 520
soma total das notas = SR+ SA => 924 + 520 = 1444
media total = 1444 /20 = 0,72
Media total da sala MT = soma total / 20 => 1444/20 = 72,2
- Agora o problema é depois que ele adiciona 5 pontos para todos ficando:
reprovados 8 x 5 = 40 => 520 + 40 = 560 na soma total
aprovados 12X 5 =60 => 924+60 = 984 na soma total
e MR fica =68,8
e MA fica = 80
nao consigo sair disso.
como o cara consegue saber que 3 alunos conseguiram a aprovacao com esses 5 pontos
VAlew