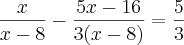
Eu até encontrei uma resposta mas não sei se está correta.
Obrigado.
por dolmian » Seg Dez 10, 2012 20:35
por e8group » Seg Dez 10, 2012 21:49
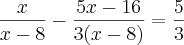
.Assim ,podemos multiplicar os membros da esquerda da igualdade por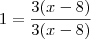 
que nos leva a ![\frac{1}{3(x-8)} \left[ 3x - (5x -16)\right] =\frac{1}{3(x-8)} \left[ -2x +16\right] = \frac{-2}{3(x-8)} \left[ x -8 \right] = \frac{-2}{3}](/latexrender/pictures/1102a945e44e5b93718165b169adeb83.png "\frac{1}{3(x-8)} \left[ 3x - (5x -16)\right] =\frac{1}{3(x-8)} \left[ -2x +16\right] = \frac{-2}{3(x-8)} \left[ x -8 \right] = \frac{-2}{3}")
.Perceba que ,desenvolvendo o lado esquerdo da equação inicial chegamos em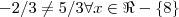 
.Portanto não há solução , logo 
.
por santiago alves » Sex Jul 08, 2011 08:46
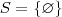Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)