Estou no início do estudo de Limites com duas variáveis. Vejam essa resolução de um exemplo do Guidorizzi (Um curso de Cálculo, vol. 2, 5 ed.).
Calcule, caso exista,
 .
.Solução
Seja f(x,y) =
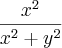 e tomemos
e tomemos  e
e  .
.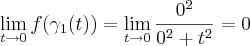
e

Logo,
 não existe.
não existe.-----------------------------------------------------------------------------------------------------
Gostaria de saber se posso tomar também
 e
e  .
.Assim, terei

e
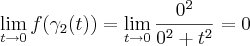
Portanto, o limite dado não existe.
Está correto?




![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)