 por guisaulo » Qui Nov 29, 2012 12:36
por guisaulo » Qui Nov 29, 2012 12:36
Seja W o subespaço de

gerado pelos vetores:
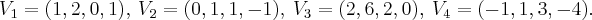
a) Mostre que os vetores
são linearmente dependentes.
Até onde cheguei:Bastaria mostrar que o determinante desses vetores deve ser igual a zero.
Porém, preciso saber quais vetores são combinação linear dentre eles para descarta-los e encontrar a base e dimensão de W.(letra b)
Para isso, fiz o escalonamento e encontrei o seguinte resultado (-2z+w, -2z-3w, z, w) sendo que z e w são variáveis livres.
Resolvendo a equação obtive
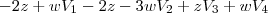
Neste caso, não consegui desenvolver a equação para encontrar quais dos vetores pode ser escrito com combinação linear dos outros.
Pode ser que errei alguma conta, mas não sei como fazer o exercício a partir desse ponto.
-
guisaulo
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Nov 27, 2012 21:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
 por MarceloFantini » Sex Nov 30, 2012 00:13
por MarceloFantini » Sex Nov 30, 2012 00:13
Ao invés do determinante, eu calcularia

, onde

são constantes. Como o conjunto tem que ser linearmente dependente, isto significa que pelo menos uma dessas constantes é não-nula, logo o conjunto é linearmente dependente.
Não existe um vetor particular que é combinação linear dos outros. Retire um e veja o que acontece com o conjunto restante. Julgando pelas coordenadas, eu diria que

é combinação linear das outras, pelo menos é o que mais parece.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Vetores LI e LD - Subespaço Gerado
por Cicero ferreira » Sex Mar 14, 2014 18:13
- 0 Respostas
- 2047 Exibições
- Última mensagem por Cicero ferreira

Sex Mar 14, 2014 18:13
Álgebra I para Licenciatura
-
- [Subespaço Vetorial] Subespaço envolvendo matrizes
por hyge » Qua Mai 02, 2018 17:04
- 2 Respostas
- 10984 Exibições
- Última mensagem por adauto martins

Dom Mai 06, 2018 12:28
Álgebra Linear
-
- [Subespaço Vetorial] Verificar que é o conjunto é subespaço
por anderson_wallace » Seg Dez 30, 2013 17:56
- 3 Respostas
- 4680 Exibições
- Última mensagem por Renato_RJ

Ter Dez 31, 2013 14:00
Álgebra Linear
-
- [VETORES]Alguém me ajuda com vetores?
por LAZAROTTI » Seg Set 17, 2012 00:49
- 2 Respostas
- 7363 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 11:28
Geometria Analítica
-
- [Vetores] Módulo e Versor de vetores
por LAZAROTTI » Sáb Set 22, 2012 22:42
- 1 Respostas
- 2988 Exibições
- Última mensagem por young_jedi

Sáb Set 22, 2012 22:50
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 gerado pelos vetores:
gerado pelos vetores: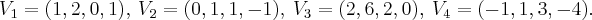
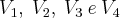 são linearmente dependentes.
são linearmente dependentes.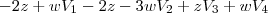


 , onde
, onde  são constantes. Como o conjunto tem que ser linearmente dependente, isto significa que pelo menos uma dessas constantes é não-nula, logo o conjunto é linearmente dependente.
são constantes. Como o conjunto tem que ser linearmente dependente, isto significa que pelo menos uma dessas constantes é não-nula, logo o conjunto é linearmente dependente. é combinação linear das outras, pelo menos é o que mais parece.
é combinação linear das outras, pelo menos é o que mais parece.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
