 por Yasmin Cristina » Qua Nov 21, 2012 11:21
por Yasmin Cristina » Qua Nov 21, 2012 11:21
Olá, gostaria de uma ajuda nesse exercício:
A soma das raízes reais da equação
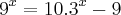
é igual a:
a) 0
b)2
c)3
d)9
e)10
OBS. a resposta é "B"
cheguei até a equação abaixo:
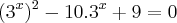
a partir daí eu não sei mais como resolver com essas exponenciais no meio...
=/
-
Yasmin Cristina
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Out 31, 2012 23:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Qua Nov 21, 2012 11:30
por Cleyson007 » Qua Nov 21, 2012 11:30
Olá Yasmin!
Tente resolver reescrevendo dessa forma:

Att,
cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Yasmin Cristina » Qua Nov 21, 2012 11:58
por Yasmin Cristina » Qua Nov 21, 2012 11:58
Professor, ainda não estou conseguindo resolver, mesmo da forma que vc me sugeriu..
Também tentei fatorar colocando o

em evidência....mas mesmo assim não deu certo..
=/
-
Yasmin Cristina
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Out 31, 2012 23:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Qua Nov 21, 2012 13:52
por Cleyson007 » Qua Nov 21, 2012 13:52
Olá Yasmin!
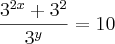
Fazendo

, temos:
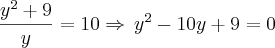
Resolvendo essa equação do 2° grau, encontramos:

e

Como estipulamos que

, temos:
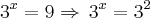
Cortando as bases -->

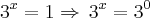
Cortando as bases, temos:

Soma das raizes:

Comente qualquer dúvida

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Yasmin Cristina » Qua Nov 21, 2012 14:19
por Yasmin Cristina » Qua Nov 21, 2012 14:19
Aii meu Deus!! era só isso?!!
Tah perfeitoo... entendii agr.. ^^
-
Yasmin Cristina
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Out 31, 2012 23:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Qua Nov 21, 2012 14:28
por Cleyson007 » Qua Nov 21, 2012 14:28
Ok Yasmin!
Era só isso mesmo

Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1624 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2836 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2826 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2239 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2190 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
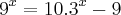 é igual a:
é igual a: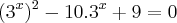

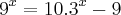 é igual a:
é igual a: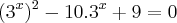



 em evidência....mas mesmo assim não deu certo..
em evidência....mas mesmo assim não deu certo..
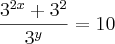
 , temos:
, temos: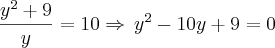
 e
e 
 , temos:
, temos: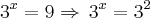

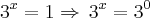








 .
.



