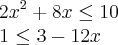
Podemos afirmar que no quadro final de medalhas a Espanha ficou com:
a) 5 medalhas de ouro, 10 de prata e 3 de bronze
b) 4 medalhas de ouro, 8 de prata e 3 de bronze
c) 7 medalhas de ouro, 14 de prata e 5 de bronze
d) 6 medalhas de ouro, 12 de prata e 5 de bronze
e) 3 medalhas de ouro, 6 de prata e 1 de bronze
Na resolução do sistema pede-se a soma dos numeros inteiros que representam a equação.
Usei o sistema 2x² + 8x - 10 = 0
+ 2 - 12x = 0
Obtive 2x² -4x - 8 = 0
a Soma das raízes é
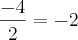
Como

Entao não haveria um antecessor impar.
RESPOSTA: Letra A


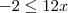 e daí
e daí 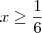 . Da primeira equação temos que dividindo tudo por dois segue que
. Da primeira equação temos que dividindo tudo por dois segue que  . Somando 4 a cada lado temos
. Somando 4 a cada lado temos 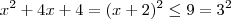 e portanto
e portanto  , obtendo a seguinte desigualdade:
, obtendo a seguinte desigualdade: 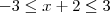 e
e 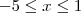 .
. 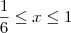 . A única solução inteira é
. A única solução inteira é  , mas
, mas 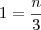 , logo
, logo  e a Espanha obteve 3 medalhas de ouro. Pelos dados do enunciado segue que ela teve 6 medalhas de prata e uma medalha de bronze.
e a Espanha obteve 3 medalhas de ouro. Pelos dados do enunciado segue que ela teve 6 medalhas de prata e uma medalha de bronze. como a soma de inteiros, o que é impossível.
como a soma de inteiros, o que é impossível. é a terça parte do "oposto" do número que representa a soma. O que ele quer dizer por "oposto"? Seria inverso multiplicativo? Se for, a resolução permanece. Agora, inverso aditivo também não está fazendo sentido, a menos que a soma das soluções inteiras fosse negativa, o que não está acontecendo. Penso um pouco mais amanhã.
é a terça parte do "oposto" do número que representa a soma. O que ele quer dizer por "oposto"? Seria inverso multiplicativo? Se for, a resolução permanece. Agora, inverso aditivo também não está fazendo sentido, a menos que a soma das soluções inteiras fosse negativa, o que não está acontecendo. Penso um pouco mais amanhã.







 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
