 por e8group » Seg Nov 12, 2012 21:45
por e8group » Seg Nov 12, 2012 21:45
Pessoal , deparei com uma questão elementar que me fez questionar sobre algo . Através de uma igualdade , nós elevamos ambos lados da igualdade ao quadrado e manteremos a igualdade verdadeira . Será mesmo ? Na minha opinião isto não vale para todos os casos .
Por exemplo , segue uma questão a seguir que o objetivo é identificar o erro na solução feito por um aluno .
Dada a inequação modular
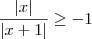
Solução.
i)

ii)
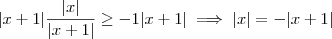
iii)
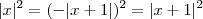
iv) Como
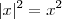
e

Segue que
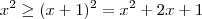
que da como solução
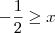
Não tenho o gabarito , mas analisando acredito que o erro está na etapa ( iii) . Não estou conseguindo formula um argumento que prove o erro dele . Por favor , alguém descorda ? Se não , qual argumento você usaria ?
Entretanto quando eu começo desenvolver a questão desde o ponto inicial , eu consigo mostrar que todos valores reais exceto

satisfaz
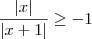
. Como segue a segue os passos a seguir .
De fato ,
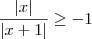
. Pois ,
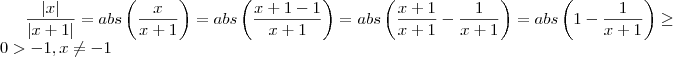
.
Quando
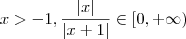
e quando
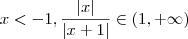
, ou seja para quaisquer
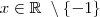
temos que
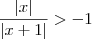
OBS. Usei abs para modulo , por causa da configuração da barra .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Seg Nov 12, 2012 21:51
por e8group » Seg Nov 12, 2012 21:51
OBS .:
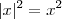
e

. Isso é verdade , mas
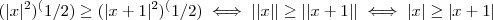
.O que não é verdade para x diferente que - 1 .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Seg Nov 12, 2012 22:11
por MarceloFantini » Seg Nov 12, 2012 22:11
Primeiro,
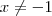
. Segundo, já está errado na segunda etapa. Teremos
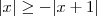
, não igual. Tome

. Então é claro que
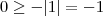
, mas
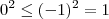
, não maior ou igual. Então o processo de elevar ao quadrado está errado.
Basta perceber que

,
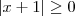
e portanto
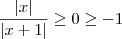
para todo
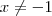
. Agora, existe outra forma, bem mais trabalhosa.
Para resolver, considere a função nos seguintes intervalos:
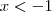
,
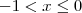
e

.
No primeiro intervalo teremos
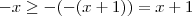
, daí
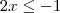
e
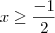
. Como assumimos
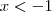
, todo valor aqui é solução.
No segundo intervalo teremos
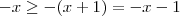
, que nos leva a
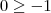
que é verdadeiro sempre. Portanto
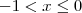
são soluções.
No terceiro e último intervalo teremos
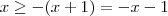
, que nos leva a

e
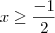
. Como assumimos

, todo valor é solução.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Seg Nov 12, 2012 22:27
por e8group » Seg Nov 12, 2012 22:27
Peço desculpas digitei errado na segunda etapa é maior ou igual , não igual . Agradeço muito , gostei muito da resolução .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7396 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- inequação modular
por manuoliveira » Dom Ago 22, 2010 22:30
- 1 Respostas
- 3480 Exibições
- Última mensagem por Dan

Seg Ago 23, 2010 15:38
Álgebra Elementar
-
- Inequação modular
por scggomes » Qui Abr 21, 2011 17:22
- 3 Respostas
- 3219 Exibições
- Última mensagem por MarceloFantini

Qui Abr 21, 2011 20:54
Cálculo: Limites, Derivadas e Integrais
-
- Inequação Modular
por Rafael16 » Qui Mar 08, 2012 20:24
- 2 Respostas
- 2418 Exibições
- Última mensagem por Rafael16

Qui Mar 08, 2012 21:21
Funções
-
- inequação modular
por haiashi » Qua Jun 06, 2012 00:33
- 0 Respostas
- 1549 Exibições
- Última mensagem por haiashi

Qua Jun 06, 2012 00:33
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
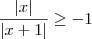

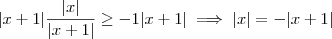
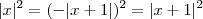
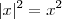 e
e  Segue que
Segue que 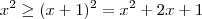 que da como solução
que da como solução 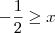
 satisfaz
satisfaz 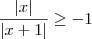 . Como segue a segue os passos a seguir .
. Como segue a segue os passos a seguir . 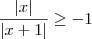 . Pois ,
. Pois , 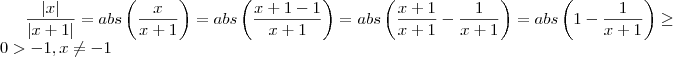 .
. 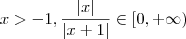 e quando
e quando 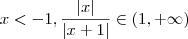 , ou seja para quaisquer
, ou seja para quaisquer 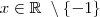 temos que
temos que 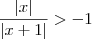


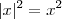 e
e  . Isso é verdade , mas
. Isso é verdade , mas 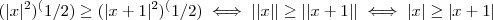 .O que não é verdade para x diferente que - 1 .
.O que não é verdade para x diferente que - 1 .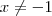 . Segundo, já está errado na segunda etapa. Teremos
. Segundo, já está errado na segunda etapa. Teremos 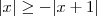 , não igual. Tome
, não igual. Tome  . Então é claro que
. Então é claro que 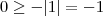 , mas
, mas 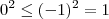 , não maior ou igual. Então o processo de elevar ao quadrado está errado.
, não maior ou igual. Então o processo de elevar ao quadrado está errado. ,
, 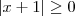 e portanto
e portanto 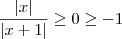 para todo
para todo 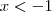 ,
, 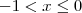 e
e  .
.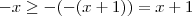 , daí
, daí 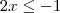 e
e 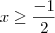 . Como assumimos
. Como assumimos 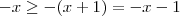 , que nos leva a
, que nos leva a 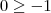 que é verdadeiro sempre. Portanto
que é verdadeiro sempre. Portanto 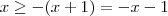 , que nos leva a
, que nos leva a  e
e  , todo valor é solução.
, todo valor é solução.



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.