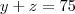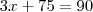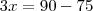por thamaracm » Sáb Nov 10, 2012 06:44
por thamaracm » Sáb Nov 10, 2012 06:44
Pessoal,
Trago uma questão de nível fácil da UFSC, porém não consegui resolver a questão número 16. Uma ajudinha, please!
25) Assinale no cartão-resposta a soma dos números associados à(s) proposição(ões) CORRETA(S).
01. Dizer que a multiplicação de dois números negativos tem por resultado um número positivo é uma afirmação sem justificativa e que nada tem a ver com questões práticas.
02. O conjunto dos números racionais é suficiente para medir (com exatidão) todo e qualquer comprimento.
04. Seja x um número inteiro diferente de zero. A existência do inverso multiplicativo de x só é garantida no conjunto dos números reais e no conjunto dos números complexos (já que R c).
08. Os números como e p (e outros irracionais) só estão relacionados a coisas abstratas e “distantes” da nossa realidade.
16. Se no último aniversário de João, a soma de sua idade com a de seu pai e a de seu avô era 90 anos, e no dia de seu nascimento esta soma era 75 anos, então João está com 5 anos.
Gabarito; 16
-
thamaracm
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Nov 09, 2012 21:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino Medio
- Andamento: formado
 por young_jedi » Sáb Nov 10, 2012 10:20
por young_jedi » Sáb Nov 10, 2012 10:20
vamos dizer que a idade de joão é x
quando joao nasceu a idade de seu pai era y
e a de seu avo z
portanto
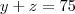
no ultimo aniversario de joao ele tinha a idade x seu pai tera a idade y+x pois quando joao nasceu ele tinha y
e seu avo tera idade z+x porque quando joao nasceu ele tinha z
então a soma das idades sera


mai nos ja sabemos que
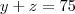
então
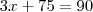
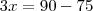


-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ufsc 2007
por manuoliveira » Seg Dez 13, 2010 21:45
- 2 Respostas
- 10964 Exibições
- Última mensagem por analauraa_b

Seg Mar 27, 2023 21:47
Geometria Plana
-
- Prisma ufsc 1996
 por Maria Livia » Sáb Nov 10, 2012 10:25
por Maria Livia » Sáb Nov 10, 2012 10:25
- 2 Respostas
- 12821 Exibições
- Última mensagem por Maria Livia

Sáb Nov 10, 2012 10:47
Geometria Espacial
-
- [potência] Questao UFSC
 por yuripa » Seg Ago 17, 2015 01:46
por yuripa » Seg Ago 17, 2015 01:46
- 3 Respostas
- 2950 Exibições
- Última mensagem por nakagumahissao

Ter Ago 18, 2015 03:15
Aritmética
-
- algebra l
por ehrefundini » Qui Mar 05, 2009 08:34
- 1 Respostas
- 7462 Exibições
- Última mensagem por Molina

Qui Mar 05, 2009 21:50
Álgebra
-
- algebra
por uspsilva » Sex Mar 13, 2009 13:03
- 1 Respostas
- 3206 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 15:22
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.