 por Biah m » Sex Nov 02, 2012 14:58
por Biah m » Sex Nov 02, 2012 14:58
Olá! Eu tenho que resolver esse exercício, porém eu não sei usar números complexos. Já procurei exemplo de resolução em livros, internet, tudo, mas tudo que eu encontro é com reais :/ Portanto, eu realmente espero que vocês possam me ajudar nessa, e me mostrar como resolver com número complexo. Muito obrigada!!!
-> Determine o núcleo e a imagem das seguinte transformação linear:
T: C²

R² dada por T (x+yi , z+ti) = (x+2z , -x+2t)
-
Biah m
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 02, 2012 14:47
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Sex Nov 02, 2012 16:26
por MarceloFantini » Sex Nov 02, 2012 16:26
Para encontrar o núcleo, faça

, então

. Resolva o sistema.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Biah m » Sex Nov 02, 2012 16:39
por Biah m » Sex Nov 02, 2012 16:39
MarceloFantini escreveu:Para encontrar o núcleo, faça

, então

. Resolva o sistema.
Eu sei resolver pros reais, mas não pros complexos. Eu resolvo o sistema e substituo como???
O sistema dará z = -x/2 e t=x/2.
Eu substituo como, então? w = (x + 0yi, -x/2 + x/2i) ???? E em seguida, o que eu faço?
Obrigada.
-
Biah m
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 02, 2012 14:47
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Sex Nov 02, 2012 16:59
por MarceloFantini » Sex Nov 02, 2012 16:59
Você encontrou então que os elementos em
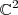
da forma

levam a transformação no zero. É só escrever isso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vualas » Sex Nov 09, 2012 13:38
por vualas » Sex Nov 09, 2012 13:38
E a imagem Marcelo?
-
vualas
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Nov 07, 2012 00:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Transformação Linear] - Como descobrir a base sem números
 por verona95 » Qua Dez 03, 2014 12:11
por verona95 » Qua Dez 03, 2014 12:11
- 3 Respostas
- 1974 Exibições
- Última mensagem por adauto martins

Qui Dez 04, 2014 10:32
Álgebra Linear
-
- [Transformação Linear] Nucleo e Imagem, ache a transformaçao
por vualas » Qua Nov 07, 2012 00:37
- 2 Respostas
- 4247 Exibições
- Última mensagem por adauto martins

Qui Dez 15, 2016 11:12
Álgebra Linear
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17104 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10526 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11558 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 R² dada por T (x+yi , z+ti) = (x+2z , -x+2t)
R² dada por T (x+yi , z+ti) = (x+2z , -x+2t)
 R² dada por T (x+yi , z+ti) = (x+2z , -x+2t)
R² dada por T (x+yi , z+ti) = (x+2z , -x+2t)
 , então
, então  . Resolva o sistema.
. Resolva o sistema.

, então
. Resolva o sistema.

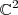 da forma
da forma  levam a transformação no zero. É só escrever isso.
levam a transformação no zero. É só escrever isso.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.