 por mih123 » Qui Nov 08, 2012 03:41
por mih123 » Qui Nov 08, 2012 03:41
Ooii,

Eu não sei muito a respeito de T.V. M (taxa de variação média), tem uma questão que é, pra você aplicar T. V. M na função

no intervalo [-2,2].
Se alguém puder me ajudar.
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Nov 08, 2012 04:05
por MarceloFantini » Qui Nov 08, 2012 04:05
Você pode digitar o enunciado completo, sem alterações? Porque a sigla T.V.M. normalmente em cálculo significa Teorema do Valor Médio, que diz que dada uma função

contínua em
![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
e derivável em

, então existe
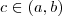
tal que
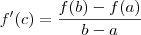
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por mih123 » Qui Nov 08, 2012 04:30
por mih123 » Qui Nov 08, 2012 04:30
Coloquei errado, realmente é o teorema do valor médio.
''É possível aplicar o T. V. M. na função f(x)=

no intervalo [-2,2].Caso afirmativo verificar-lo.''
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Nov 08, 2012 04:38
por MarceloFantini » Qui Nov 08, 2012 04:38
Verifique então se esta função é contínua no intervalo fechado e derivável no intervalo aberto. Se estas duas condições forem satisfeitas, vale o teorema do valor médio. Dica: se existir um problema, será com
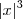
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por mih123 » Qui Nov 08, 2012 04:59
por mih123 » Qui Nov 08, 2012 04:59
Eu fiz f(-2)=
![\frac{{\left[x \right]}^{3}}{1+{x}^{6}} \frac{{\left[x \right]}^{3}}{1+{x}^{6}}](/latexrender/pictures/b7fb5c09981506fa9e7a918290d1b693.png)
= 8/65

= 8/65
Devo fazer o que mais?
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Nov 08, 2012 05:02
por MarceloFantini » Qui Nov 08, 2012 05:02
Isto não prova nada, você apenas calculou a função nos extremos. Sendo mais direto, ver que é contínua é fácil pois é composição e divisão de funções contínuas, portanto contínua. Você precisa demonstrar agora que ela é derivável em todos os pontos do intervalo
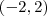
. Para isto, derive e veja se a expressão é derivável em todos os pontos do intervalo dito.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por mih123 » Qui Nov 08, 2012 05:28
por mih123 » Qui Nov 08, 2012 05:28
Estou com sérios problemas relacionados à derivada com modulo. ;/
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Nov 08, 2012 05:34
por MarceloFantini » Qui Nov 08, 2012 05:34
A derivada do módulo é

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por mih123 » Qui Nov 08, 2012 10:18
por mih123 » Qui Nov 08, 2012 10:18
f '(x)= 0 ?
-
mih123
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Seg Ago 27, 2012 03:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Nov 08, 2012 16:50
por MarceloFantini » Qui Nov 08, 2012 16:50
O que você quer dizer com isso?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11058 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Dúvida PA
por Cleyson007 » Dom Jun 01, 2008 01:01
- 2 Respostas
- 10770 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Progressões
-
- Dúvida
por miguelbaptista » Sex Jan 09, 2009 03:29
- 8 Respostas
- 12551 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:13
Logaritmos
-
- dúvida
por gdarius » Dom Ago 16, 2009 00:09
- 1 Respostas
- 3159 Exibições
- Última mensagem por Felipe Schucman

Dom Ago 16, 2009 02:35
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida!!
por GABRIELA » Qui Set 17, 2009 18:19
- 5 Respostas
- 5739 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 no intervalo [-2,2].
no intervalo [-2,2].

 no intervalo [-2,2].
no intervalo [-2,2].
 contínua em
contínua em ![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) e derivável em
e derivável em  , então existe
, então existe 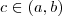 tal que
tal que 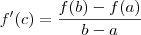 .
.

 no intervalo [-2,2].Caso afirmativo verificar-lo.''
no intervalo [-2,2].Caso afirmativo verificar-lo.''
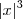 .
.

![\frac{{\left[x \right]}^{3}}{1+{x}^{6}} \frac{{\left[x \right]}^{3}}{1+{x}^{6}}](/latexrender/pictures/b7fb5c09981506fa9e7a918290d1b693.png) = 8/65
= 8/65 = 8/65
= 8/65
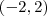 . Para isto, derive e veja se a expressão é derivável em todos os pontos do intervalo dito.
. Para isto, derive e veja se a expressão é derivável em todos os pontos do intervalo dito.










