 por rafaeldouglas » Dom Out 28, 2012 22:12
por rafaeldouglas » Dom Out 28, 2012 22:12
Olá pessoal eu sou novo aqui e estou com dúvida nesta questão :
Considere o sistema linear Ax = b, onde
1 2 0 3
A = 0 0 0 0 e b = (b1; b2; b3)T
2 4 0 1
(a) Sob que condi�ções de b, o sistema tem solu�ção?
(b) Encontre uma base para o espa�ço nulo de A?
(c) Encontre a solu�ção geral para Ax = b (quando existir uma)
(d) Encontre uma base para o espa�co coluna (espa�co formado pelas
colunas de A).
Se tiver algum material explicando como se faz o passo a passo eu agradeço tbm !
Grato e espero respostas !?
Ps :Este T que fica (b1; b2; b3)T significa a Transposta
-
rafaeldouglas
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Out 28, 2012 21:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo de Informação(TI)
- Andamento: cursando
 por MarceloFantini » Dom Out 28, 2012 22:43
por MarceloFantini » Dom Out 28, 2012 22:43
Rafael Douglas, por favor atente para as regras do fórum, em especial a regra número 2. Além disso, se a matriz for como escreveu, o enunciado está errado. Você tem uma matriz

multiplicada por uma matriz, à direita, que é
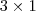
. Logo, se o sistema é
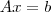
, então provavelmente a matriz

é
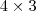
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rafaeldouglas » Dom Out 28, 2012 23:05
por rafaeldouglas » Dom Out 28, 2012 23:05
Po eu tentei seguir a regra 2 escrever o formulario mas não consegui ( desistir ) mas tem como me dá um auxilo nesta questão (só fornecendo como se resolve) ou ?
Editado pela última vez por
rafaeldouglas em Dom Out 28, 2012 23:30, em um total de 1 vez.
-
rafaeldouglas
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Out 28, 2012 21:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo de Informação(TI)
- Andamento: cursando
 por MarceloFantini » Dom Out 28, 2012 23:14
por MarceloFantini » Dom Out 28, 2012 23:14
Faltaram apenas os comandos
- Código: Selecionar todos
[tex][/tex]
antes e depois do se código. Você continuou não observando o que eu disse: a matriz que você escreveu, novamente, é

. Isto significa que ela tem três linhas e quatro colunas, e para multiplicar por outra matriz á direita, esta deve ter
quatro linhas. A matriz

que você escreveu tem apenas
três, portanto não é possível fazer a multiplicação.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3081 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4487 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- [SISTEMA] problema que envolve um sistema
por brunnkpol » Qui Jan 02, 2014 22:57
- 2 Respostas
- 2704 Exibições
- Última mensagem por brunnkpol

Seg Jan 06, 2014 21:37
Sistemas de Equações
-
- [Sistema linear] Sistema linear com constante
por smlspirit » Qui Jul 19, 2012 19:34
- 4 Respostas
- 5544 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 22:40
Sistemas de Equações
-
- sistema
por Jessi » Seg Abr 20, 2009 16:56
- 1 Respostas
- 2043 Exibições
- Última mensagem por Marcampucio

Seg Abr 20, 2009 18:08
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 multiplicada por uma matriz, à direita, que é
multiplicada por uma matriz, à direita, que é 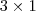 . Logo, se o sistema é
. Logo, se o sistema é 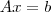 , então provavelmente a matriz
, então provavelmente a matriz  é
é  .
.

 que você escreveu tem apenas
que você escreveu tem apenas