 por cristian9192 » Qui Out 25, 2012 14:02
por cristian9192 » Qui Out 25, 2012 14:02
Estou refazendo um de integral tripla so que tranquei em uma reção trigonometrica que não consigo entender:

que se transforama em:
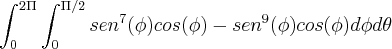
Se algué poder me dar uma dica de como se faz essa transformação, agradeço!
-
cristian9192
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Out 19, 2012 02:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Qui Out 25, 2012 14:46
por young_jedi » Qui Out 25, 2012 14:46
separe em duas integrais

voce usa integração por substituição
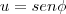

então a integral fica
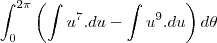
faça a integral depois volte para a variavel

e aplique os limites , depois faça a integral para

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por cristian9192 » Qui Out 25, 2012 14:55
por cristian9192 » Qui Out 25, 2012 14:55
Na verdade o que eu não intendo é como isso:

Se transforma nisso:

-
cristian9192
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Out 19, 2012 02:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Out 25, 2012 14:57
por e8group » Qui Out 25, 2012 14:57
Note que ,
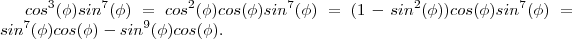
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por cristian9192 » Qui Out 25, 2012 15:32
por cristian9192 » Qui Out 25, 2012 15:32
Obrigado pessoal, consegui enteder e a cabar a integral.
Abraço.
-
cristian9192
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Out 19, 2012 02:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral Dupla com trasformação trigonométrica
por cristian9192 » Sáb Out 20, 2012 19:06
- 1 Respostas
- 877 Exibições
- Última mensagem por young_jedi

Sáb Out 20, 2012 21:40
Cálculo: Limites, Derivadas e Integrais
-
- Integral Tripla
por Cleyson007 » Qua Mai 16, 2012 11:41
- 2 Respostas
- 2088 Exibições
- Última mensagem por LuizAquino

Sex Mai 18, 2012 20:14
Cálculo: Limites, Derivadas e Integrais
-
- Integral tripla
por DanielFerreira » Dom Jun 10, 2012 19:27
- 1 Respostas
- 1700 Exibições
- Última mensagem por Russman

Seg Jun 11, 2012 00:39
Cálculo: Limites, Derivadas e Integrais
-
- INTEGRAL TRIPLA
por Garota nerd » Qua Jun 27, 2012 17:40
- 4 Respostas
- 3135 Exibições
- Última mensagem por Garota nerd

Qui Jun 28, 2012 01:28
Cálculo: Limites, Derivadas e Integrais
-
- Integral tripla
por DanielFerreira » Sáb Jul 07, 2012 13:00
- 2 Respostas
- 1877 Exibições
- Última mensagem por DanielFerreira

Dom Jul 08, 2012 13:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

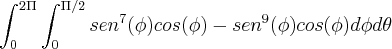


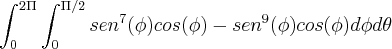


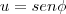

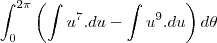
 e aplique os limites , depois faça a integral para
e aplique os limites , depois faça a integral para 






 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.