 por gedersoncruz » Sáb Out 20, 2012 19:07
por gedersoncruz » Sáb Out 20, 2012 19:07
Calcule utilizando integrais duplas:
A área da região do plano xOy limitado pelas curvas
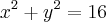
e

.
Rta:
![\frac{16\sqrt[2]{3}}{3}+4 \frac{16\sqrt[2]{3}}{3}+4](/latexrender/pictures/b4292dc00163efbfd53687aa57269cb5.png)
Tentei fazer e obtive os seguintes limites de integração porém não chego neste resultado. Utilizei os seguintes limites:
![\int_{0}^{2\sqrt[2]{3}}\int_{\frac{{y}^{2}}{3}}^{4-y}.dx.dy \int_{0}^{2\sqrt[2]{3}}\int_{\frac{{y}^{2}}{3}}^{4-y}.dx.dy](/latexrender/pictures/f10091b1a359d6ea946d0aa7520c6dd7.png)
Desde já agradecido.
-
gedersoncruz
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Out 20, 2012 18:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Sáb Out 20, 2012 21:32
por young_jedi » Sáb Out 20, 2012 21:32
eu acho que a integral fica assim

se entendi bem é isso, qualquer coisa pergunte
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por gedersoncruz » Dom Out 21, 2012 00:14
por gedersoncruz » Dom Out 21, 2012 00:14
young_jedi eu tentei resolve esta integral mas não consegui obter o resultado certo, teria como você mostrar a solução?
-
gedersoncruz
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Out 20, 2012 18:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por gedersoncruz » Dom Out 21, 2012 11:30
por gedersoncruz » Dom Out 21, 2012 11:30
Qual identidade trigonométrica você utilizou para obter esta expressão
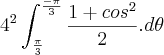
?
-
gedersoncruz
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Out 20, 2012 18:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Dom Out 21, 2012 11:38
por young_jedi » Dom Out 21, 2012 11:38
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por gedersoncruz » Dom Out 21, 2012 11:45
por gedersoncruz » Dom Out 21, 2012 11:45
Nossa! Muito obrigado. Já vou dar uma revisada na trigonometria. Valeu mesmo.
-
gedersoncruz
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Out 20, 2012 18:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral dupla
por DanielFerreira » Sex Mar 16, 2012 23:56
- 2 Respostas
- 2578 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 17, 2012 19:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 2
por DanielFerreira » Dom Mar 18, 2012 12:44
- 5 Respostas
- 3931 Exibições
- Última mensagem por DanielFerreira

Sex Mar 23, 2012 22:34
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 4
 por DanielFerreira » Sex Abr 06, 2012 19:49
por DanielFerreira » Sex Abr 06, 2012 19:49
- 4 Respostas
- 2926 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 21:05
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 5
por DanielFerreira » Sex Abr 06, 2012 20:00
- 2 Respostas
- 1790 Exibições
- Última mensagem por DanielFerreira

Sex Abr 06, 2012 20:16
Cálculo: Limites, Derivadas e Integrais
-
- Integral dupla - 6
 por DanielFerreira » Sáb Abr 14, 2012 22:54
por DanielFerreira » Sáb Abr 14, 2012 22:54
- 1 Respostas
- 1357 Exibições
- Última mensagem por LuizAquino

Dom Abr 15, 2012 23:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
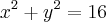 e
e  .
.![\frac{16\sqrt[2]{3}}{3}+4 \frac{16\sqrt[2]{3}}{3}+4](/latexrender/pictures/b4292dc00163efbfd53687aa57269cb5.png)
![\int_{0}^{2\sqrt[2]{3}}\int_{\frac{{y}^{2}}{3}}^{4-y}.dx.dy \int_{0}^{2\sqrt[2]{3}}\int_{\frac{{y}^{2}}{3}}^{4-y}.dx.dy](/latexrender/pictures/f10091b1a359d6ea946d0aa7520c6dd7.png)

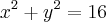 e
e  .
.![\frac{16\sqrt[2]{3}}{3}+4 \frac{16\sqrt[2]{3}}{3}+4](/latexrender/pictures/b4292dc00163efbfd53687aa57269cb5.png)
![\int_{0}^{2\sqrt[2]{3}}\int_{\frac{{y}^{2}}{3}}^{4-y}.dx.dy \int_{0}^{2\sqrt[2]{3}}\int_{\frac{{y}^{2}}{3}}^{4-y}.dx.dy](/latexrender/pictures/f10091b1a359d6ea946d0aa7520c6dd7.png)







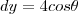
 temos
temos 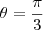 e
e temos
temos 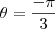
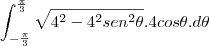

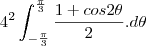
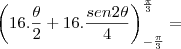

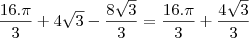

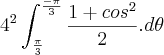 ?
?
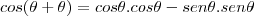
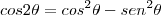
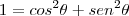




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.