 por Jhonata » Sex Out 05, 2012 18:24
por Jhonata » Sex Out 05, 2012 18:24
Bem, estou nas minhas primeiras semanas de aulas de álgebra linear e só agora fui enfrentar os livros. Bem, algumas coisas eu acho que tá dando pra levar, outras estou encontrando mais dificuldade, enfim, eu me deparei com um problema, consegui desenvolver algumas coisas mas não chego a resposta final.
Eis a questão:
Determine o ponto de interseção dos pares abaixo, caso exista, caso contrário, justifique:
a)dos planos

e

;
Observando os dois planos, dá pra ver que preciso de um parâmetro pra equação do segundo. E só sei que é um plano porque o problema diz, como não confundir com uma reta, caso o problema não diga nada?
Prosseguindo... Eu dei um parâmetro pra segunda equação, da seguinte forma:
Colocando z = t, e substituindo de volta na equação anterior, obtive x = 1+ t e logo substitui essas informações na primeira equação(a do plano que foi dada) obtive:
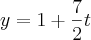
Tá... E agora? Devo descobrir o valor de t pra depois descobrir o valor das variáveis x, y e z?
A resposta do problema é a seguinte: a interseção destes 2 planos é a reta {(1 , 1, 0) + t(1, 7/2, 1}| t pertence a R}.
Notei que há uma parcialidade do valor em y nessa reta... Mas o que faço para obter os outros valores que estão descritos nessa reta? Foi isso que não entendi, além das outras dúvidas citadas acima... Por favor, me ajudem. Obrigado desde já!
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por LuizAquino » Sex Out 05, 2012 19:01
por LuizAquino » Sex Out 05, 2012 19:01
Jhonata escreveu:Determine o ponto de interseção dos pares abaixo, caso exista, caso contrário, justifique:
a)dos planos

e

;
Jhonata escreveu:Observando os dois planos, dá pra ver que preciso de um parâmetro pra equação do segundo. E só sei que é um plano porque o problema diz, como não confundir com uma reta, caso o problema não diga nada?
Vai depender do contexto no qual o exercício foi proposto.
Por exemplo, se estamos falando de pontos no plano (ou seja, em

), então a equação x - z = 1 representa uma reta no plano xOz (aqui O representa a origem do sistema).
Mas se estamos falando de pontos no espaço (ou seja, em

), então a equação x - z = 1 representa um plano.
Jhonata escreveu:Prosseguindo... Eu dei um parâmetro pra segunda equação, da seguinte forma:
Colocando z = t, e substituindo de volta na equação anterior, obtive x = 1+ t e logo substitui essas informações na primeira equação(a do plano que foi dada) obtive:
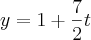
Tá... E agora? Devo descobrir o valor de t pra depois descobrir o valor das variáveis x, y e z?
A resposta do problema é a seguinte: a interseção destes 2 planos é a reta {(1 , 1, 0) + t(1, 7/2, 1}| t pertence a R}.
Notei que há uma parcialidade do valor em y nessa reta... Mas o que faço para obter os outros valores que estão descritos nessa reta? Foi isso que não entendi, além das outras dúvidas citadas acima...
Não precisa (e nem faria sentido) "descobrir o valor de t". A variável t representa justamente o parâmetro, que será um número real qualquer escolhido.
Apenas resumindo o que você fez até aqui, note que você poderia escrever:

Isso representa as equações paramétricas de uma reta.
Agora perceba que uma outra forma de escrever isso é justamente como está no gabarito:
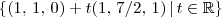
.
Detalhe: esse exercício possui infinitas respostas, já que existem infinitas equações paramétricas que representam uma mesma reta. Caso você tivesse escolhido, por exemplo, começar fixando y = t, então você teria obtido outra resposta igualmente válida:

Essa resposta também poderia ser escrita como:

.
ObservaçãoEu gostaria de recomendar que você assista a videoaula "13. Geometria Analítica - Equações da Reta". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Jhonata » Sáb Out 06, 2012 13:22
por Jhonata » Sáb Out 06, 2012 13:22
LuizAquino escreveu:Jhonata escreveu:Determine o ponto de interseção dos pares abaixo, caso exista, caso contrário, justifique:
a)dos planos

e

;
Jhonata escreveu:Observando os dois planos, dá pra ver que preciso de um parâmetro pra equação do segundo. E só sei que é um plano porque o problema diz, como não confundir com uma reta, caso o problema não diga nada?
Vai depender do contexto no qual o exercício foi proposto.
Por exemplo, se estamos falando de pontos no plano (ou seja, em

), então a equação x - z = 1 representa uma reta no plano xOz (aqui O representa a origem do sistema).
Mas se estamos falando de pontos no espaço (ou seja, em

), então a equação x - z = 1 representa um plano.
Jhonata escreveu:Prosseguindo... Eu dei um parâmetro pra segunda equação, da seguinte forma:
Colocando z = t, e substituindo de volta na equação anterior, obtive x = 1+ t e logo substitui essas informações na primeira equação(a do plano que foi dada) obtive:
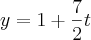
Tá... E agora? Devo descobrir o valor de t pra depois descobrir o valor das variáveis x, y e z?
A resposta do problema é a seguinte: a interseção destes 2 planos é a reta {(1 , 1, 0) + t(1, 7/2, 1}| t pertence a R}.
Notei que há uma parcialidade do valor em y nessa reta... Mas o que faço para obter os outros valores que estão descritos nessa reta? Foi isso que não entendi, além das outras dúvidas citadas acima...
Não precisa (e nem faria sentido) "descobrir o valor de t". A variável t representa justamente o parâmetro, que será um número real qualquer escolhido.
Apenas resumindo o que você fez até aqui, note que você poderia escrever:

Isso representa as equações paramétricas de uma reta.
Agora perceba que uma outra forma de escrever isso é justamente como está no gabarito:
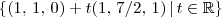
.
Detalhe: esse exercício possui infinitas respostas, já que existem infinitas equações paramétricas que representam uma mesma reta. Caso você tivesse escolhido, por exemplo, começar fixando y = t, então você teria obtido outra resposta igualmente válida:

Essa resposta também poderia ser escrita como:

.
ObservaçãoEu gostaria de recomendar que você assista a videoaula "13. Geometria Analítica - Equações da Reta". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
Entendi toda sua explicação, além do vídeo muito esclarecedor...
Eu tenho acompanhado seus videos desde que decidi mergulhar no mundo das exatas e eles tem me ajudado muito até aqui.
Não existem palavras para agradecer o seu grandioso trabalho Luiz, meus parabéns e muito, muito obrigado mesmo. Continue sendo esse excelente professor que é, mais principalmente, a perfeita pessoa que é.
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3427 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equaçoes parametricas
por angels900 » Ter Jan 31, 2012 14:35
- 6 Respostas
- 3722 Exibições
- Última mensagem por LuizAquino

Ter Jan 31, 2012 17:04
Geometria Analítica
-
- Equações paramétricas da curva
por kalschne » Qui Fev 16, 2012 20:51
- 3 Respostas
- 2113 Exibições
- Última mensagem por kalschne

Qui Fev 16, 2012 22:48
Geometria Analítica
-
- [Equações Paramétricas - Espaço]
por raimundoocjr » Ter Set 24, 2013 20:40
- 2 Respostas
- 1863 Exibições
- Última mensagem por raimundoocjr

Qua Set 25, 2013 19:05
Cálculo: Limites, Derivadas e Integrais
-
- Faz sentido? Sistema e equações paramétricas.
por Dan » Ter Fev 01, 2011 14:39
- 4 Respostas
- 3754 Exibições
- Última mensagem por LuizAquino

Qua Fev 02, 2011 11:37
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  ;
;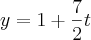


 ), então a equação x - z = 1 representa uma reta no plano xOz (aqui O representa a origem do sistema).
), então a equação x - z = 1 representa uma reta no plano xOz (aqui O representa a origem do sistema). ), então a equação x - z = 1 representa um plano.
), então a equação x - z = 1 representa um plano.
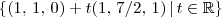 .
.
 .
.





