 é
é R:

Galera me ajuda aew por favor, ñ sei nem por onde começar a fazer este tipo de questão desde já muito agradecido...

 é
é 

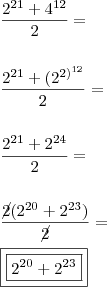


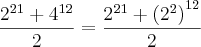
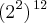
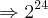 (Conserva-se a base e multiplica os expontes)
(Conserva-se a base e multiplica os expontes)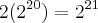 (Conserva-se a base e soma os expoentes)
(Conserva-se a base e soma os expoentes) (Aqui aplica-se a mesma regra que usamos anteriormente)
(Aqui aplica-se a mesma regra que usamos anteriormente)




Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
