 por mayconf » Sex Set 28, 2012 14:54
por mayconf » Sex Set 28, 2012 14:54
Galera num to conseguindo chegar no resultado certo desse limite
![\lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} \lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x}](/latexrender/pictures/19ad56d9ea5a963747bfcb1400c2e50f.png)
eu fiz assim num sei si ta certo
![\lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} .\frac{\sqrt[]{1+x}+\sqrt[]{1-x}}{\sqrt[]{1+x}+\sqrt[]{1-x}}\Rightarrow \frac{1+x-1-x}{x\left(\sqrt[]{1+x}+\sqrt[]{1-x} \right)}\Rightarrow\frac{1-1-x}{\sqrt[]{1+x}+\sqrt[]{1-x}} \lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} .\frac{\sqrt[]{1+x}+\sqrt[]{1-x}}{\sqrt[]{1+x}+\sqrt[]{1-x}}\Rightarrow \frac{1+x-1-x}{x\left(\sqrt[]{1+x}+\sqrt[]{1-x} \right)}\Rightarrow\frac{1-1-x}{\sqrt[]{1+x}+\sqrt[]{1-x}}](/latexrender/pictures/37ae33f376aa5d6f8c7e3cdc7fe66de0.png)
-
mayconf
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sex Set 21, 2012 12:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sex Set 28, 2012 16:18
por LuizAquino » Sex Set 28, 2012 16:18
mayconf escreveu:Galera num to conseguindo chegar no resultado certo desse limite
![\lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} \lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x}](/latexrender/pictures/19ad56d9ea5a963747bfcb1400c2e50f.png)
eu fiz assim num sei si ta certo
![\lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} .\frac{\sqrt[]{1+x}+\sqrt[]{1-x}}{\sqrt[]{1+x}+\sqrt[]{1-x}}\Rightarrow \frac{1+x-1-x}{x\left(\sqrt[]{1+x}+\sqrt[]{1-x} \right)}\Rightarrow\frac{1-1-x}{\sqrt[]{1+x}+\sqrt[]{1-x}} \lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} .\frac{\sqrt[]{1+x}+\sqrt[]{1-x}}{\sqrt[]{1+x}+\sqrt[]{1-x}}\Rightarrow \frac{1+x-1-x}{x\left(\sqrt[]{1+x}+\sqrt[]{1-x} \right)}\Rightarrow\frac{1-1-x}{\sqrt[]{1+x}+\sqrt[]{1-x}}](/latexrender/pictures/37ae33f376aa5d6f8c7e3cdc7fe66de0.png)
Note que:
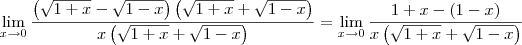
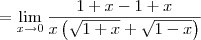
Agora continue a partir daí.
ObservaçãoProcure usar a notação de modo adequado. Na notação de limite não escrevemos x = 0, mas sim
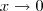
. Além disso, enquanto você está resolvendo esse limite, você deve escrever a notação

em todos os passos, exceto no último quando você já calcula o valor do limite.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por mayconf » Sex Set 28, 2012 18:19
por mayconf » Sex Set 28, 2012 18:19
eu corto um "x" de cima com um de baixo certo? ai em cima fica 1-1+x, que ficaria x?
-
mayconf
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sex Set 21, 2012 12:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Sex Set 28, 2012 18:33
por LuizAquino » Sex Set 28, 2012 18:33
mayconf escreveu:eu corto um "x" de cima com um de baixo certo? ai em cima fica 1-1+x, que ficaria x?
Errado! Você não pode "cortar" o termo x da forma como você quer, pois há uma sequência de somas e subtrações no numerador. Primeiro você precisa resolver essas operações para depois efetuar as devidas
simplificações (evite usar o termo "cortar").
Temos então o seguinte:
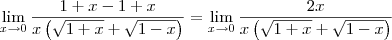
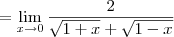
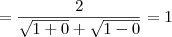
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por mayconf » Sáb Set 29, 2012 16:31
por mayconf » Sáb Set 29, 2012 16:31
Valeu ae LuizAquino, brigadão mesmo me salvou
-
mayconf
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sex Set 21, 2012 12:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por gabriel feron » Dom Set 30, 2012 20:07
por gabriel feron » Dom Set 30, 2012 20:07
Estou fazendo a mesma questão, o que tive dificuldade nela, foi na parte de cima, que por erro meu acabou dando 1+x-1-x, por erro de matemática simples, por isso não fechava, mas agora consegui! valeuu mesmo!
-
gabriel feron
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Seg Abr 16, 2012 03:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Hídrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite - como resolver um lim quando temos raiz^2 e raiz^3.
por Monica santos » Sex Ago 16, 2013 14:22
- 4 Respostas
- 4134 Exibições
- Última mensagem por young_jedi

Sex Ago 16, 2013 19:01
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo: limite com raiz dentro de raiz
 por roberto_trebor » Sáb Fev 15, 2014 20:45
por roberto_trebor » Sáb Fev 15, 2014 20:45
- 1 Respostas
- 2240 Exibições
- Última mensagem por Man Utd

Dom Fev 16, 2014 17:58
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] raiz
por beel » Ter Set 06, 2011 13:48
- 5 Respostas
- 2609 Exibições
- Última mensagem por beel

Sex Set 09, 2011 16:52
Cálculo: Limites, Derivadas e Integrais
-
- Limite com Raiz
por Thyago Quimica » Sex Mai 25, 2012 18:08
- 1 Respostas
- 1390 Exibições
- Última mensagem por Guill

Sex Mai 25, 2012 20:03
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE]raiz/ duvida
por beel » Dom Set 11, 2011 15:09
- 6 Respostas
- 2934 Exibições
- Última mensagem por beel

Dom Out 16, 2011 16:59
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} \lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x}](/latexrender/pictures/19ad56d9ea5a963747bfcb1400c2e50f.png)
![\lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} .\frac{\sqrt[]{1+x}+\sqrt[]{1-x}}{\sqrt[]{1+x}+\sqrt[]{1-x}}\Rightarrow \frac{1+x-1-x}{x\left(\sqrt[]{1+x}+\sqrt[]{1-x} \right)}\Rightarrow\frac{1-1-x}{\sqrt[]{1+x}+\sqrt[]{1-x}} \lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} .\frac{\sqrt[]{1+x}+\sqrt[]{1-x}}{\sqrt[]{1+x}+\sqrt[]{1-x}}\Rightarrow \frac{1+x-1-x}{x\left(\sqrt[]{1+x}+\sqrt[]{1-x} \right)}\Rightarrow\frac{1-1-x}{\sqrt[]{1+x}+\sqrt[]{1-x}}](/latexrender/pictures/37ae33f376aa5d6f8c7e3cdc7fe66de0.png)

![\lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} \lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x}](/latexrender/pictures/19ad56d9ea5a963747bfcb1400c2e50f.png)
![\lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} .\frac{\sqrt[]{1+x}+\sqrt[]{1-x}}{\sqrt[]{1+x}+\sqrt[]{1-x}}\Rightarrow \frac{1+x-1-x}{x\left(\sqrt[]{1+x}+\sqrt[]{1-x} \right)}\Rightarrow\frac{1-1-x}{\sqrt[]{1+x}+\sqrt[]{1-x}} \lim_{x=0}\frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} .\frac{\sqrt[]{1+x}+\sqrt[]{1-x}}{\sqrt[]{1+x}+\sqrt[]{1-x}}\Rightarrow \frac{1+x-1-x}{x\left(\sqrt[]{1+x}+\sqrt[]{1-x} \right)}\Rightarrow\frac{1-1-x}{\sqrt[]{1+x}+\sqrt[]{1-x}}](/latexrender/pictures/37ae33f376aa5d6f8c7e3cdc7fe66de0.png)

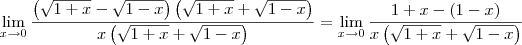
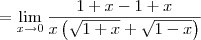
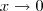 . Além disso, enquanto você está resolvendo esse limite, você deve escrever a notação
. Além disso, enquanto você está resolvendo esse limite, você deve escrever a notação  em todos os passos, exceto no último quando você já calcula o valor do limite.
em todos os passos, exceto no último quando você já calcula o valor do limite.

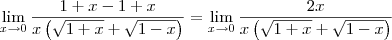
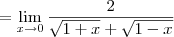
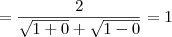




 .
.



