Sejam r e s retas reversas passando or A e B e por C e D, respectivamente. Obtenha uma equação vetorial para a reta l concorrente com r e s e que é paralela ao vetor v(1,-5,-1) onde A(0,1,0) , B(1,1,0) , C (-3,1,-4) e D(-1,2, -7)
Da reta r, o vetor diretor seria o AB=(1,0,0)
Da reta s, o vetor diretor seria o CD=(2,1,-3)
r: (0,1,0) + t(1,0,0)
s: (-3,1,-4) +s(2,1,-3)
Eu teria que achar um ponto de interseção entre r e l , e entre s e l para daí eu fazer um vetor (ex.: ponto M e N , fazer o vetor MN) e formar a equação??
Alguém tem ideia de como se faz? Não consigo achar um ponto em comum entre essas retas...


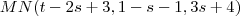


 =1
=1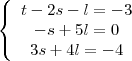
 (1,-5,-1)
(1,-5,-1) em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.