 por Paraujo » Dom Set 23, 2012 21:15
por Paraujo » Dom Set 23, 2012 21:15
Boa noite Pessoal,
Estou relembrando alguns conceitos de derivada e precisava desenvolver a derivada abaixo para um experimento físico:
![\frac{\partial q}{\partial\theta} = \sqrt[]{\frac{{(sen \theta)}^{3}}{cos \theta}} \frac{\partial q}{\partial\theta} = \sqrt[]{\frac{{(sen \theta)}^{3}}{cos \theta}}](/latexrender/pictures/6b9ac49838cc42bc75006c3975000a05.png)
Obrigado pela ajuda!
-
Paraujo
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 23, 2012 21:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão
- Andamento: cursando
 por young_jedi » Dom Set 23, 2012 21:25
por young_jedi » Dom Set 23, 2012 21:25
você quer encontrar a função
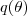
apartir da equação?
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Russman » Dom Set 23, 2012 21:46
por Russman » Dom Set 23, 2012 21:46
Isto é uma equação diferencial parcial do tipo

cuja solução é
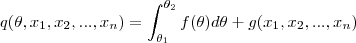
onde

é uma possível variável de dependência de

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Paraujo » Dom Set 23, 2012 21:49
por Paraujo » Dom Set 23, 2012 21:49
Na verdade essa é uma derivada parcial de um cálculo de propagação de erro, a minha dúvida está no desenvolvimento dela, não me recordo como resolver um derivada desse tipo.
Obrigado!
-
Paraujo
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 23, 2012 21:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão
- Andamento: cursando
 por Russman » Dom Set 23, 2012 22:28
por Russman » Dom Set 23, 2012 22:28
Você qer derivar a função

, é isso?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Paraujo » Dom Set 23, 2012 23:31
por Paraujo » Dom Set 23, 2012 23:31
Isso mesmo... Não me recordo a tratativa em casos onde temos funções dentro de uma raiz e etc...
-
Paraujo
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 23, 2012 21:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão
- Andamento: cursando
 por Russman » Seg Set 24, 2012 01:16
por Russman » Seg Set 24, 2012 01:16
Basta aplicar as regras da Cadeia e do Quociente.

Agora, para funções do tipo
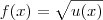
temos
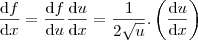
Basta calcular as derivadas das funções raízes que aparecem e substituir na fórmula.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Paraujo » Ter Set 25, 2012 11:12
por Paraujo » Ter Set 25, 2012 11:12
Obrigado Russman!!
Estou meio confuso no meu resultado, a fórmula é uma multiplicação de uma constante (positiva) pelo rsultado dessa derivada, cheguei num resultado negativo, e é nesse ponto que achei estranho, nesse contexto minha variação seria negativa... Você pode conferir essa derivada abaixo por favor?

Abraço
Paulo
-
Paraujo
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 23, 2012 21:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão
- Andamento: cursando
 por young_jedi » Ter Set 25, 2012 11:49
por young_jedi » Ter Set 25, 2012 11:49
pela regra da derivada do quociente

no entanto voce inverteu a ordem
por isso sua derivada deu com o sinal invertido
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Paraujo » Ter Set 25, 2012 12:15
por Paraujo » Ter Set 25, 2012 12:15
Perfeito Jedi! Obrigado!!
-
Paraujo
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 23, 2012 21:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12552 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- Derivada do Quociente
 por dekol2 » Dom Mai 06, 2012 20:39
por dekol2 » Dom Mai 06, 2012 20:39
- 4 Respostas
- 4290 Exibições
- Última mensagem por LuizAquino

Seg Mai 07, 2012 11:34
Cálculo: Limites, Derivadas e Integrais
-
- Derivada quociente.
por Sobreira » Seg Out 29, 2012 16:24
- 3 Respostas
- 2903 Exibições
- Última mensagem por young_jedi

Seg Out 29, 2012 17:58
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida com derivada do quociente
por arnoanderson » Seg Nov 02, 2009 12:08
- 2 Respostas
- 3862 Exibições
- Última mensagem por arnoanderson

Ter Nov 03, 2009 09:36
Cálculo: Limites, Derivadas e Integrais
-
- Exercício Derivada do Quociente
por Tayron » Qua Fev 09, 2011 16:35
- 1 Respostas
- 5450 Exibições
- Última mensagem por LuizAquino

Qua Fev 09, 2011 17:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\partial q}{\partial\theta} = \sqrt[]{\frac{{(sen \theta)}^{3}}{cos \theta}} \frac{\partial q}{\partial\theta} = \sqrt[]{\frac{{(sen \theta)}^{3}}{cos \theta}}](/latexrender/pictures/6b9ac49838cc42bc75006c3975000a05.png)

![\frac{\partial q}{\partial\theta} = \sqrt[]{\frac{{(sen \theta)}^{3}}{cos \theta}} \frac{\partial q}{\partial\theta} = \sqrt[]{\frac{{(sen \theta)}^{3}}{cos \theta}}](/latexrender/pictures/6b9ac49838cc42bc75006c3975000a05.png)

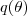 apartir da equação?
apartir da equação?

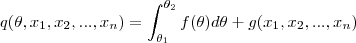
 é uma possível variável de dependência de
é uma possível variável de dependência de  .
.




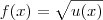
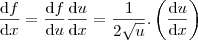







 .
.
 :
: